Giải Toán 12 trang 42 Tập 1 Cánh diều

---

Với Giải Toán 12 trang 42 Tập 1 trong Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số Toán 12 Cánh diều hay nhất, chi tiết sẽ giúp học sinh lớp 12 dễ dàng làm bài tập Toán 12 trang 42.

Giải Toán 12 trang 42 Tập 1 Cánh diều

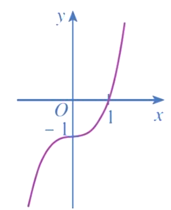
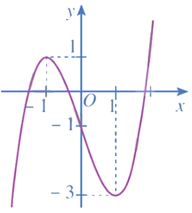
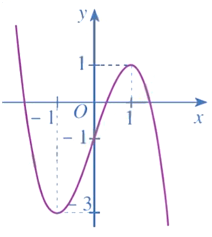
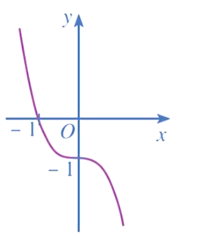
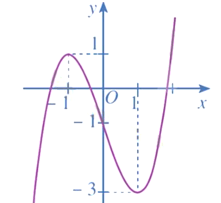
Bài 1 trang 42 Toán 12 Tập 1: Đồ thị hàm số y = x³ – 3x – 1 là đường cong nào trong các đường cong sau?

A.

B.

C.

D.

Lời giải:

Đáp án đúng là: B

Hàm số đã cho có tập xác định là ℝ.

Ta có y' = 3x² – 3;

          y' = 0 ⇔ x = – 1 hoặc x = 1.

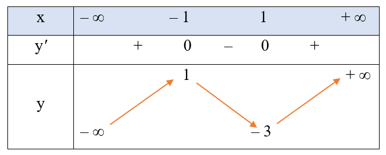
Bảng biến thiên của hàm số là

 Do đó, đồ thị của hàm số y = x³ – 3x – 1 là

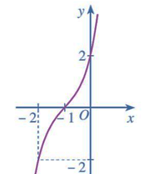
Bài 2 trang 42 Toán 12 Tập 1: Đường cong ở Hình 29 là đồ thị của hàm số:

A. y = x³ + x² + 2x + 2.  

B. y = – x³ – 4x² – x + 2.

C. y = x³ + 3x² – 4x + 2.

D. y = x³ + 3x² + 4x + 2.

Lời giải:

Đáp án đúng là: D

Ta thấy đồ thị hàm số đi lên từ trái qua phải nên loại đáp án B.

Đồ thị hàm số đi qua điểm (– 2; – 2) nên thay vào các đáp án ta loại được đáp án A và đáp án C. Vậy đường cong trong Hình 29 là đồ thị hàm số ở đáp án D.

Lời giải bài tập Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số hay khác:

• Giải Toán 12 trang 28
• Giải Toán 12 trang 43
• Giải Toán 12 trang 44