Bài 7 trang 27 Toán 12 Tập 2 Chân trời sáng tạo

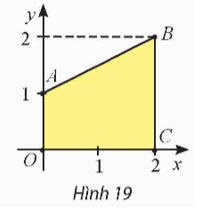
Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2) và C(2; 0) (Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục Ox.

Giải Toán 12 Bài 3: Ứng dụng hình học của tích phân - Chân trời sáng tạo

Bài 7 trang 27 Toán 12 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2) và C(2; 0) (Hình 19). Tính thể tích khối tròn xoay tạo thành khi quay hình thang OABC quanh trục Ox.

Lời giải:

Ta có OABC là hình thang vuông, có đường cao OC nằm trên trục Ox.

Khi quay hình thang OABC quanh trục Ox ta được khối tròn xoay là khối nón cụt, có bán kính đáy bé r₁ = OA = 1, bán kính đáy lớn r₂ = BC = 2 và chiều cao h = OC = 2.

Thể tích cần tính là:

$V=\frac{1}{3}\pi \left(r_1^2+r_1{r}_2+r_2^2\right)h=\frac{1}{3}\pi \left(1^2+1.2+2^2\right).2=\frac{14\pi }{3}$

Lời giải bài tập Toán 12 Bài 3: Ứng dụng hình học của tích phân hay, chi tiết khác:

• Hoạt động khởi động trang 21 Toán 12 Tập 2: Ta đã biết công thức tính thể tích của khối cầu bán kính R là $V=\frac{4\pi R^3}{3}$. Làm thế nào để tìm ra công thức đó? ....

• Hoạt động khám phá 1 trang 21 Toán 12 Tập 2: Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S₁ là diện tích hình phẳng giới hạn bởi d ....

• Thực hành 1 trang 22 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x – x², trục hoành và hai đường thẳng x = 0, x = 3 ....

• Thực hành 2 trang 22 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = cosx – 2, trục hoành và hai đường thẳng x = 0, x = π ....

• Hoạt động khám phá 2 trang 23 Toán 12 Tập 2: Cho hai hàm số y = 4x – x² và y = x lần lượt có đồ thị (P) và d như Hình 4 ....

• Thực hành 3 trang 24 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x² – 2x – 1, y = x – 1 và hai đường thẳng x = 1, x = 4 ....

• Thực hành 4 trang 24 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = 5x − x², y = x² – x và hai đường thẳng x = 0, x = 2 ....

• Vận dụng 1 trang 24 Toán 12 Tập 2: Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 7 ....

• Hoạt động khám phá 3 trang 24 Toán 12 Tập 2: Trong không gian, cho hình chóp O.ABCD có đáy là hình vuông cạnh a, OA  (ABCD) ....

• Thực hành 5 trang 25 Toán 12 Tập 2: Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao x (dm) (0 ≤ x ≤ 4) ....

• Hoạt động khám phá 4 trang 25 Toán 12 Tập 2: Cho D là hình phẳng giới hạn bởi đồ thị hàm số $y=f\left(x\right)=\frac{1}{2}x$, trục hoành và đường thẳng x = 4 ....

• Thực hành 6 trang 26 Toán 12 Tập 2: Gọi D là hình phẳng giới hạn bởi đồ thị hàm số $y=1+\frac{1}{x}$, trục hoành và hai đường thẳng x = 1, x = 2 ....

• Vận dụng 2 trang 27 Toán 12 Tập 2: Sử dụng tích phân, tính thể tích khối nón có bán kính đáy r và chiều cao h (Hình 16) ....

• Bài 1 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi ....

• Bài 2 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = x³ – x, trục hoành và hai đường thẳng x = 0, x = 2 ....

• Bài 3 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số $y=\frac{x^2+1}{x}$, y = – x và hai đường thẳng x = 1, x = 4 ....

• Bài 4 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x³ + 1, y = 2 và hai đường thẳng x = −1, x = 2 ....

• Bài 5 trang 27 Toán 12 Tập 2: Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−2 ≤ x ≤ 2) ....

• Bài 6 trang 27 Toán 12 Tập 2: Cho D là hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{4-x}$ (x ≤ 4), trục tung và trục hoành (Hình 18) ....

• Bài 8 trang 27 Toán 12 Tập 2: Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h (Hình 20) ....