Bài 8 trang 27 Toán 12 Tập 2 Chân trời sáng tạo

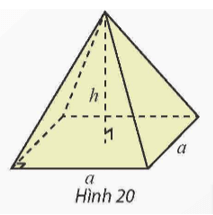
Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h (Hình 20).

Giải Toán 12 Bài 3: Ứng dụng hình học của tích phân - Chân trời sáng tạo

Bài 8 trang 27 Toán 12 Tập 2: Sử dụng tích phân, tính thể tích của hình chóp tứ giác đều có cạnh đáy bằng a và chiều cao bằng h (Hình 20).

Lời giải:

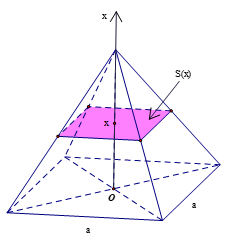
Chọn trục Ox trùng với đường cao của hình chóp đều như hình vẽ, sao cho mặt đáy nằm trong mặt phẳng vuông góc với trục Ox tại x = 0.

Mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 ≤ x ≤ h) cắt hình chóp đều theo mặt cắt là hình vuông đồng dạng với đáy của hình chóp theo tỉ số $\frac{x}{h}$.

Do đó $\frac{S\left(x\right)}{a^2}={\left(\frac{x}{h}\right)}^2$$\Rightarrow S\left(x\right)={\left(\frac{x}{h}\right)}^2{a}^2=\frac{a^2}{h^2}{x}^2$.

Do đó thể tích khối chóp tứ giác đều là:

$V=\underset{0}{\overset{h}{\int }}\frac{a^2}{h^2}{x}^{2}dx$$={\left.\left(\frac{a^2}{h^2}.\frac{x^3}{3}\right)\right|}_0^h=\frac{1}{3}{a}^{2}h$

Lời giải bài tập Toán 12 Bài 3: Ứng dụng hình học của tích phân hay, chi tiết khác:

• Hoạt động khởi động trang 21 Toán 12 Tập 2: Ta đã biết công thức tính thể tích của khối cầu bán kính R là $V=\frac{4\pi R^3}{3}$. Làm thế nào để tìm ra công thức đó? ....

• Hoạt động khám phá 1 trang 21 Toán 12 Tập 2: Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S₁ là diện tích hình phẳng giới hạn bởi d ....

• Thực hành 1 trang 22 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x – x², trục hoành và hai đường thẳng x = 0, x = 3 ....

• Thực hành 2 trang 22 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = cosx – 2, trục hoành và hai đường thẳng x = 0, x = π ....

• Hoạt động khám phá 2 trang 23 Toán 12 Tập 2: Cho hai hàm số y = 4x – x² và y = x lần lượt có đồ thị (P) và d như Hình 4 ....

• Thực hành 3 trang 24 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x² – 2x – 1, y = x – 1 và hai đường thẳng x = 1, x = 4 ....

• Thực hành 4 trang 24 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = 5x − x², y = x² – x và hai đường thẳng x = 0, x = 2 ....

• Vận dụng 1 trang 24 Toán 12 Tập 2: Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 7 ....

• Hoạt động khám phá 3 trang 24 Toán 12 Tập 2: Trong không gian, cho hình chóp O.ABCD có đáy là hình vuông cạnh a, OA  (ABCD) ....

• Thực hành 5 trang 25 Toán 12 Tập 2: Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao x (dm) (0 ≤ x ≤ 4) ....

• Hoạt động khám phá 4 trang 25 Toán 12 Tập 2: Cho D là hình phẳng giới hạn bởi đồ thị hàm số $y=f\left(x\right)=\frac{1}{2}x$, trục hoành và đường thẳng x = 4 ....

• Thực hành 6 trang 26 Toán 12 Tập 2: Gọi D là hình phẳng giới hạn bởi đồ thị hàm số $y=1+\frac{1}{x}$, trục hoành và hai đường thẳng x = 1, x = 2 ....

• Vận dụng 2 trang 27 Toán 12 Tập 2: Sử dụng tích phân, tính thể tích khối nón có bán kính đáy r và chiều cao h (Hình 16) ....

• Bài 1 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi ....

• Bài 2 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = x³ – x, trục hoành và hai đường thẳng x = 0, x = 2 ....

• Bài 3 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số $y=\frac{x^2+1}{x}$, y = – x và hai đường thẳng x = 1, x = 4 ....

• Bài 4 trang 27 Toán 12 Tập 2: Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x³ + 1, y = 2 và hai đường thẳng x = −1, x = 2 ....

• Bài 5 trang 27 Toán 12 Tập 2: Khi cắt một vật thể hình chiếc nêm bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (−2 ≤ x ≤ 2) ....

• Bài 6 trang 27 Toán 12 Tập 2: Cho D là hình phẳng giới hạn bởi đồ thị hàm số $y=\sqrt{4-x}$ (x ≤ 4), trục tung và trục hoành (Hình 18) ....

• Bài 7 trang 27 Toán 12 Tập 2: Trong mặt phẳng tọa độ Oxy, cho hình thang OABC có A(0; 1), B(2; 2) và C(2; 0) (Hình 19) ....