Bài 7 trang 57 Toán 12 Tập 1 Chân trời sáng tạo

Giải Toán 12 Bài 2: Toạ độ của vectơ trong không gian - Chân trời sáng tạo

Bài 7 trang 57 Toán 12 Tập 1: Ở một sân bay, vị trí của máy bay được xác định bởi điểm M trong không gian Oxyz như Hình 17. Gọi H là hình chiếu vuông góc của M xuống mặt phẳng (Oxy). Cho biết OM = 50, $\left(\overrightarrow{i},\overrightarrow{OH}\right)=64°$, $\left(\overrightarrow{OH},\overrightarrow{OM}\right)=48°$. Tìm tọa độ của điểm M.

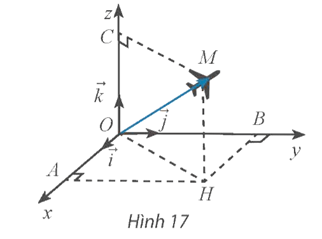
Lời giải:

Giả sử M(x; y; z).

H $\in$ (Oxy) $\Rightarrow$ H(x; y; 0).

Vì OBHA là hình bình hành nên BH = OA.

Vì OCMH là hình bình hành nên OC = MH.

Xét $∆$MHO vuông tại H, có OH = OM.cos48° = 50. cos48° ≈ 33,46.

MH = OM.sin48° = 50. sin48° ≈ 37,16.

Xét $∆$OAH vuông tại A, có BH = OA = OH.cos64° = 33,46. cos64° ≈ 14,67.

Xét $∆$OBH vuông tại B, có $OB=\sqrt{O{H}^2-B{H}^2}=\sqrt{33,{46}^2-14,{67}^2}\approx 30,07$ .

Vì $\overrightarrow{OA}$ và $\overrightarrow{i}$ cùng hướng và OA = 14,67 nên $\overrightarrow{OA}=14,67\overrightarrow{i}$ .

Vì $\overrightarrow{OB}$ và $\overrightarrow{j}$ cùng hướng và OB = 30,07 nên $\overrightarrow{OB}=30,07\overrightarrow{j}$ .

Vì $\overrightarrow{OC}$ và $\overrightarrow{k}$ cùng hướng và OC = 37,16 nên $\overrightarrow{OC}=37,16\overrightarrow{k}$ .

Áp dụng quy tắc hình bình hành, ta có:

$\overrightarrow{OM}=\overrightarrow{OH}+\overrightarrow{OC}=\overrightarrow{OA}+\overrightarrow{OB}+\overrightarrow{OC}=14,67\overrightarrow{i}+30,07\overrightarrow{j}+27,16\overrightarrow{k}$

Vậy M(14,67; 30,07; 27,16).

Lời giải bài tập Toán 12 Bài 2: Toạ độ của vectơ trong không gian hay, chi tiết khác:

• Hoạt động khởi động trang 52 Toán 12 Tập 1: Trong kiểm soát không lưu, người ta dùng bộ ba số để xác định vị trí của máy bay. Người ta đã làm điều đó ....

• Hoạt động khám phá 1 trang 52 Toán 12 Tập 1: Cho hình lập phương OABC.O'A'B'C' có cạnh bằng 1. Đặt $\overrightarrow{i}=\overrightarrow{OA},\overrightarrow{j}=\overrightarrow{OC},\overrightarrow{k}=\overrightarrow{O{O}^{\text{'}}}$ ....

• Thực hành 1 trang 53 Toán 12 Tập 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 1, SA vuông góc với mặt phẳng đáy ....

• Vận dụng 1 trang 53 Toán 12 Tập 1: Một thiết kế cơ khí trong Hình 5a được biểu diễn trong không gian Oxyz như Hình 5b ....

• Hoạt động khám phá 2 trang 53 Toán 12 Tập 1: Cho hình hộp chữ nhật OABC.O'A'B'C' có cạnh OA = 3, OC = 5, OO' = 2 ....

• Thực hành 2 trang 54 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 5. Chọn hệ trục tọa độ Oxyz ....

• Hoạt động khám phá 3 trang 54 Toán 12 Tập 1: Trong không gian Oxyz, cho vectơ $\overrightarrow{a}$. Vẽ điểm A sao cho $\overrightarrow{OA}=\overrightarrow{a}$ . Gọi $\left(a_1;a_2;a_3\right)$  là tọa độ của điểm A ....

• Thực hành 3 trang 56 Toán 12 Tập 1: Cho hình chóp S.ABCD có đáy là hình vuông cạnh bằng 2, SA vuông góc với mặt phẳng đáy ....

• Vận dụng 2 trang 56 Toán 12 Tập 1: Một máy bay đang cất cánh từ phi trường. Với hệ tọa độ Oxyz được thiết lập ....

• Bài 1 trang 56 Toán 12 Tập 1: Trong không gian Oxyz, biết a) $\overrightarrow{a}=5\overrightarrow{i}+7\overrightarrow{j}-3\overrightarrow{k},\overrightarrow{b}=2\overrightarrow{i}+4\overrightarrow{k}$ . Tìm tọa độ các vectơ $\overrightarrow{a},\overrightarrow{b}$ ....

• Bài 2 trang 56 Toán 12 Tập 1: Trong không gian Oxyz, biết: a) $\overrightarrow{a}=\left(-2;5;-7\right)$, $\overrightarrow{b}=\left(4;0;1\right)$. Tính $\overrightarrow{a},\overrightarrow{b}$ theo các vectơ $\overrightarrow{i},\overrightarrow{j},\overrightarrow{k}$ . ....

• Bài 3 trang 56 Toán 12 Tập 1: Cho tứ diện SABC có ABC là tam giác vuông tại B, BC = 3, BA = 2, SA vuông góc với mặt phẳng ....

• Bài 4 trang 57 Toán 12 Tập 1: Cho hình chóp S.ABC có đáy ABC là tam giác đều cạnh bằng 2, SA vuông góc với đáy ....

• Bài 5 trang 57 Toán 12 Tập 1: Trong không gian Oxyz, cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh bằng 5 ....

• Bài 6 trang 57 Toán 12 Tập 1: Một chiếc xe đang kéo căng sợi dây cáp AB trong công trường xây dựng, trên đó đã thiết lập ....