Hoạt động khám phá 2 trang 43 Toán 12 Tập 1 Chân trời sáng tạo

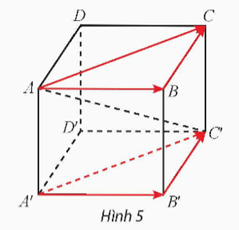
Cho hình hộp ABCD.A'B'C'D' (Hình 5).

Giải Toán 12 Bài 1: Vectơ và các phép toán trong không gian - Chân trời sáng tạo

Hoạt động khám phá 2 trang 43 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' (Hình 5).

a) Trong mặt phẳng (ABCD), tìm vectơ tổng $\overrightarrow{AB}+\overrightarrow{BC}$ .

Trong mặt phẳng (A'B'C'D'), tìm vectơ tổng $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$ .

b) Tìm mối liên hệ giữa các cặp vectơ $\overrightarrow{AB}$ và $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$ , $\overrightarrow{BC}$ và $\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$ , $\overrightarrow{AC}$ và $\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ .

c) Giải thích tại sao $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{A^{\text{'}}{B}^{\text{'}}}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}$ .

Lời giải:

a) $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ .

$\overrightarrow{A^{\text{'}}{B}^{\text{'}}}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$.

b) Vì AA'B'B là hình bình hành, suy ra AB // A'B' và AB = A'B'.

Ta có hai vectơ $\overrightarrow{AB}$ và $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$ cùng hướng và có độ dài bằng nhau nên $\overrightarrow{AB}=\overrightarrow{A^{\text{'}}{B}^{\text{'}}}$.

Tương tự: $\overrightarrow{BC}=\overrightarrow{B^{\text{'}}{C}^{\text{'}}};\overrightarrow{AC}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ .

c) Vì $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{AC}$ và $\overrightarrow{A^{\text{'}}{B}^{\text{'}}}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ mà $\overrightarrow{AC}=\overrightarrow{A^{\text{'}}{C}^{\text{'}}}$ nên $\overrightarrow{AB}+\overrightarrow{BC}=\overrightarrow{A^{\text{'}}{B}^{\text{'}}}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}.$

Lời giải bài tập Toán 12 Bài 1: Vectơ và các phép toán trong không gian hay, chi tiết khác:

• Hoạt động khởi động trang 41 Toán 12 Tập 1: Trong không gian, làm thế nào để biểu diễn độ dịch chuyển tín hiệu vô tuyến từ máy bay ....

• Hoạt động khám phá 1 trang 41 Toán 12 Tập 1: Nhắc lại định nghĩa vectơ trong mặt phẳng. Có thể định nghĩa vectơ trong không gian như ....

• Thực hành 1 trang 42 Toán 12 Tập 1: Trong hoạt động khởi động, tìm vectơ biểu diễn độ dịch chuyển tín hiệu vô tuyến từ vị trí A ....

• Thực hành 2 trang 42 Toán 12 Tập 1: Cho hình chóp tứ giác đều S.ABCD. a) Chỉ ra các vectơ có điểm đầu là S và điểm cuối ....

• Vận dụng 1 trang 43 Toán 12 Tập 1: Trong Hình 4, cho biết ba vectơ $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ biểu diễn lực căng của các sợi dây cáp AB, AC ....

• Hoạt động khám phá 3 trang 44 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. a) Tìm các vectơ tổng $\overrightarrow{AB}+\overrightarrow{AD},\overrightarrow{AC}+\overrightarrow{A{A}^{\text{'}}}$ ....

• Thực hành 3 trang 45 Toán 12 Tập 1: Cho hình hộp ABCD.EFGH. Tìm các vectơ: ....

• Hoạt động khám phá 4 trang 45 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. a) Trong mặt phẳng (ABCD), tìm vectơ hiệu $\overrightarrow{AB}-\overrightarrow{AD}$ . ....

• Thực hành 4 trang 46 Toán 12 Tập 1: Cho tứ diện ABCD có M và N lần lượt là trung điểm của AB và CD. Tìm các vectơ: ....

• Thực hành 5 trang 46 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng đơn vị. Tìm độ dài các vectơ sau đây: ....

• Vận dụng 2 trang 46 Toán 12 Tập 1: Ba lực  $\overrightarrow{F_1},\overrightarrow{F_2},\overrightarrow{F_3}$ cùng tác động vào một vật có phương đôi một vuông góc và có độ lớn ....

• Hoạt động khám phá 5 trang 46 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D' có AC' và A'C cắt nhau tại O (Hình 18) ....

• Thực hành 6 trang 47 Toán 12 Tập 1: Cho hình lăng trụ ABC.A'B'C' có M là trung điểm của BB' (Hình 20). Đặt $\overrightarrow{CA}=\overrightarrow{a}$, $\overrightarrow{CB}=\overrightarrow{b}$, $\overrightarrow{C{C}^{\text{'}}}=\overrightarrow{c}$ ....

• Vận dụng 3 trang 48 Toán 12 Tập 1: Một chiếc đèn chùm treo có khối lượng m = 5 kg được thiết kế với đĩa đèn được giữ bởi bốn đoạn xích ....

• Hoạt động khám phá 6 trang 48 Toán 12 Tập 1: a) Nhắc lại định nghĩa góc giữa hai vectơ $\overrightarrow{u}$ và $\overrightarrow{v}$ trong mặt phẳng. ....

• Thực hành 7 trang 49 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D'. Xác định góc $\left(\overrightarrow{AC},\overrightarrow{B^{\text{'}}{D}^{\text{'}}}\right)$, $\left(\overrightarrow{A^{\text{'}}A},\overrightarrow{C{B}^{\text{'}}}\right)$. ....

• Hoạt động khám phá 7 trang 49 Toán 12 Tập 1: Trong không gian, cho $\overrightarrow{u}$ và $\overrightarrow{v}$thỏa mãn $\left|\overrightarrow{u}\right|=2,\left|\overrightarrow{v}\right|=3$ . Lấy một điểm A bất kì, gọi B và C là hai điểm ....

• Thực hành 8 trang 50 Toán 12 Tập 1: Cho hình lập phương ABCD.A'B'C'D' có cạnh bằng 1 ....

• Vận dụng 4 trang 50 Toán 12 Tập 1: Một em nhỏ cân nặng m = 25 kg trượt trên cầu trượt dài 3,5 m. Biết rằng, cầu trượt có góc nghiêng ....

• Bài 1 trang 50 Toán 12 Tập 1: Cho hình hộp ABCD.A'B'C'D'. Chứng minh rằng: a) $\overrightarrow{AB}+\overrightarrow{B^{\text{'}}{C}^{\text{'}}}+\overrightarrow{D{D}^{\text{'}}}=\overrightarrow{A{C}^{\text{'}}}$; ....

• Bài 2 trang 51 Toán 12 Tập 1: Cho hình bình hành ABCD. Gọi S là một điểm không thuộc mặt phẳng chứa hình bình hành ....

• Bài 3 trang 51 Toán 12 Tập 1: Ba lực có điểm đặt tại một đỉnh của hình lập phương, cùng phương với 3 cạnh và cùng có cường độ là 5 N ....

• Bài 4 trang 51 Toán 12 Tập 1: Cho hình chóp S.ABCD. Gọi I là trọng tâm của tam giác ABC và J là trọng tâm tam giác ADC ....

• Bài 5 trang 51 Toán 12 Tập 1: Cho hình lăng trụ tam giác ABC.A'B'C' có $\overrightarrow{A{A}^{\text{'}}}=\overrightarrow{a},\overrightarrow{AB}=\overrightarrow{b},\overrightarrow{AC}=\overrightarrow{c}$. Chứng minh rằng $\overrightarrow{B^{\text{'}}C}=\overrightarrow{c}-\overrightarrow{a}-\overrightarrow{b}$ và $\overrightarrow{B{C}^{\text{'}}}=\overrightarrow{a}-\overrightarrow{b}+\overrightarrow{c}$ ....

• Bài 6 trang 51 Toán 12 Tập 1: Nếu một vật có khối lượng m (kg) thì lực hấp dẫn $\overrightarrow{P}$của Trái Đất tác dụng lên vật được xác định theo công thức ....

• Bài 7 trang 51 Toán 12 Tập 1: Trong điện trường đều, lực tĩnh điện $\overrightarrow{F}$ (đơn vị: N) tác dụng lên điện tích điểm có điện tích q (đơn vị: C)  ....

• Bài 8 trang 51 Toán 12 Tập 1: Một lực tĩnh điện $\overrightarrow{F}$tác động lên điện tích điểm M trong điện trường đều làm cho M dịch chuyển theo đường gấp khúc ....