Thực hành 1 trang 13 Toán 12 Tập 2 Chân trời sáng tạo

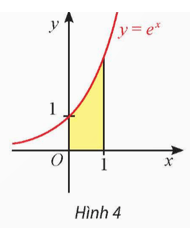
Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = e, trục hoành, trục tung và đường thẳng x = 1 (Hình 4).

Giải Toán 12 Bài 2: Tích phân - Chân trời sáng tạo

Thực hành 1 trang 13 Toán 12 Tập 2: Tính diện tích hình thang cong giới hạn bởi đồ thị hàm số y = f(x) = e^x, trục hoành, trục tung và đường thẳng x = 1 (Hình 4).

Lời giải:

Ta có hàm số y = e^x liên tục, dương trên đoạn [0; 1] .

Ta có $\int e^{x}dx=e^x+C$. Suy ra một nguyên hàm của hàm số y = e^x là F(x) = e^x.

Do đó diện tích hình thang cong cần tính là:

S = F(1) – F(0) = e – 1.

Lời giải bài tập Toán 12 Bài 2: Tích phân hay, chi tiết khác:

• Hoạt động khởi động trang 12 Toán 12 Tập 2: Một ô tô đang di chuyển với vận tốc 20 m/s thì hãm phanh nên tốc độ (m/s) của xe thay đổi theo thời gian ....

• Hoạt động khám phá 1 trang 12 Toán 12 Tập 2: Cho hàm số y = f(x) = x + 1. Với mỗi x ≥ 1, kí hiệu S(x) là diện tích của hình thang giới hạn ....

• Hoạt động khám phá 2 trang 14 Toán 12 Tập 2: Cho hàm số f(x) = 2x – 1. Lấy hai nguyên hàm tùy ý F(x) và G(x) của f(x), rồi tính F(3) – F(0) ....

• Thực hành 2 trang 16 Toán 12 Tập 2: Tính các tích phân sau: a) $\underset{1}{\overset{3}{\int }}2xdx$;       b) $\underset{0}{\overset{\pi }{\int }}\sin tdt$ ....

• Vận dụng 1 trang 16 Toán 12 Tập 2: Sau khi xuất phát, ô tô di chuyển với tốc độ $v\left(t\right)=2t-\mathrm{0,03}{t}^2\left(0\le t\le 10\right)$, trong đó v(t) tính theo m/s ....

• Hoạt động khám phá 3 trang 16 Toán 12 Tập 2: a) Tìm một nguyên hàm F(x) của hàm số f(x) = 6x⁵. Từ đó, tính $\underset{0}{\overset{2}{\int }}6x^{5}dx$ ....

• Thực hành 3 trang 17 Toán 12 Tập 2: Tính các tích phân sau: a) $\underset{-1}{\overset{1}{\int }}4x^{7}dx$;      b) $\underset{-2}{\overset{-1}{\int }}\frac{-3}{10x}dx$ ....

• Hoạt động khám phá 4 trang 17 Toán 12 Tập 2: a) Tìm một nguyên hàm F(x) của hàm số f(x) = x² + e^x. Từ đó, tính $\underset{0}{\overset{1}{\int }}\left(x^2+e^x\right)dx$ ....

• Thực hành 4 trang 18 Toán 12 Tập 2: Tính các tích phân sau: a) $\underset{1}{\overset{2}{\int }}\frac{x-1}{x^2}dx$;          b) $\underset{0}{\overset{\pi }{\int }}\left(1+2{\sin }^2\frac{x}{2}\right)dx$ ....

• Vận dụng 2 trang 18 Toán 12 Tập 2: Tại một nhà máy sản xuất một loại phân bón, gọi P(x) là lợi nhuận (tính theo triệu đồng) thu được từ việc bán x ....

• Hoạt động khám phá 5 trang 18 Toán 12 Tập 2: Cho hàm số f(x) = 2x. Tính và so sánh kết quả $\underset{0}{\overset{2}{\int }}f\left(x\right)dx$ và $\underset{0}{\overset{1}{\int }}f\left(x\right)dx+\underset{1}{\overset{2}{\int }}f\left(x\right)dx$ ....

• Thực hành 5 trang 19 Toán 12 Tập 2: Tính: a) $\underset{-1}{\overset{\frac{1}{2}}{\int }}\left(4x^3-5\right)dx-\underset{1}{\overset{\frac{1}{2}}{\int }}\left(4x^3-5\right)dx$;         b) $\underset{0}{\overset{3}{\int }}\left|x-1\right|dx$ ....

• Vận dụng 3 trang 19 Toán 12 Tập 2: Biết rằng tốc độ v (km/phút) của một ca nô cao tốc thay đổi theo thời gian t (phút) như sau ....

• Bài 1 trang 20 Toán 12 Tập 2: Tính diện tích hình thang cong giới hạn bởi ....

• Bài 2 trang 20 Toán 12 Tập 2: Tính các tích phân sau: a) $\underset{1}{\overset{2}{\int }}{x}^{4}dx$;     b)$\underset{1}{\overset{2}{\int }}\frac{1}{\sqrt{x}}dx$ ....

• Bài 3 trang 20 Toán 12 Tập 2: Tính các tích phân sau: a) $\underset{-2}{\overset{4}{\int }}\left(x+1\right)\left(x-1\right)dx$;     b) $\underset{1}{\overset{2}{\int }}\frac{x^2-2x+1}{x}dx$ ....

• Bài 4 trang 20 Toán 12 Tập 2: Tính các tích phân sau a) $\underset{-2}{\overset{1}{\int }}\left|2x+2\right|dx$;     b) $\underset{0}{\overset{4}{\int }}\left|x^2-4\right|dx$ ....

• Bài 5 trang 20 Toán 12 Tập 2: Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình 9 ....

• Bài 6 trang 20 Toán 12 Tập 2: Giả sử tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t (giây) ....