Giải Toán 12 trang 20 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 12 trang 20 Tập 2 trong Bài 2: Tích phân Toán 12 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 20.

Giải Toán 12 trang 20 Tập 2 Chân trời sáng tạo

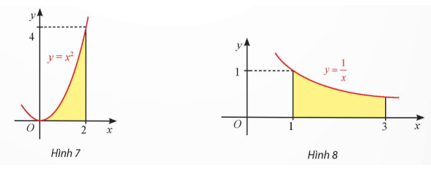
Bài 1 trang 20 Toán 12 Tập 2: Tính diện tích hình thang cong giới hạn bởi:

a) Đồ thị hàm số y = x², trục hoành và hai đường thẳng x = 0, x = 2 (Hình 7);

b) Đồ thị hàm số $y=\frac{1}{x}$, trục hoành và hai đường thẳng x = 1, x = 3 (Hình 8).

Lời giải:

a) Vì y = x² liên tục và không âm trên [0; 2] nên ta có:

$S=\underset{0}{\overset{2}{\int }}{x}^{2}dx={\left.\frac{x^3}{3}\right|}_0^2=\frac{8}{3}$.

b) Vì $y=\frac{1}{x}$ liên tục và không âm trên [1; 3] nên ta có:

$S=\underset{1}{\overset{3}{\int }}\frac{1}{x}dx={\left.\ln \left|x\right|\right|}_1^3=\ln 3-\ln 1=\ln 3$.

Bài 2 trang 20 Toán 12 Tập 2: Tính các tích phân sau:

a) $\underset{1}{\overset{2}{\int }}{x}^{4}dx$;                        b) $\underset{1}{\overset{2}{\int }}\frac{1}{\sqrt{x}}dx$; 

c) $\underset{0}{\overset{\frac{\pi }{4}}{\int }}\frac{1}{{\cos }^{2}x}dx$;                 d)$\underset{0}{\overset{2}{\int }}{3}^{x}dx$

Lời giải:

a) $\underset{1}{\overset{2}{\int }}{x}^{4}dx$$={\left.\frac{x^5}{5}\right|}_1^2=\frac{32}{5}-\frac{1}{5}=\frac{31}{5}$

b) $\underset{1}{\overset{2}{\int }}\frac{1}{\sqrt{x}}dx$$=\underset{1}{\overset{2}{\int }}{x}^{\frac{-1}{2}}dx={\left.2\sqrt{x}\right|}_1^2=2\sqrt{2}-2$

c) $\underset{0}{\overset{\frac{\pi }{4}}{\int }}\frac{1}{{\cos }^{2}x}dx$$={\left.\tan x\right|}_0^{\frac{\pi }{4}}=1$

d)$\underset{0}{\overset{2}{\int }}{3}^{x}dx$$={\left.\frac{3^x}{\ln 3}\right|}_0^2=\frac{9}{\ln 3}-\frac{1}{\ln 3}=\frac{8}{\ln 3}$

Bài 3 trang 20 Toán 12 Tập 2: Tính các tích phân sau:

a) $\underset{-2}{\overset{4}{\int }}\left(x+1\right)\left(x-1\right)dx$;                               

b) $\underset{1}{\overset{2}{\int }}\frac{x^2-2x+1}{x}dx$;   

c) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(3\sin x-2\right)dx$;         

d) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{{\sin }^{2}x}{1+\cos x}dx$

Lời giải:

a) $\underset{-2}{\overset{4}{\int }}\left(x+1\right)\left(x-1\right)dx$$=\underset{-2}{\overset{4}{\int }}\left(x^2-1\right)dx$$=\underset{-2}{\overset{4}{\int }}{x}^{2}dx-\underset{-2}{\overset{4}{\int }}dx$$={\left.\left(\frac{x^3}{3}-x\right)\right|}_{-2}^4$$=\frac{52}{3}+\frac{2}{3}=\frac{54}{3}=18$

b) $\underset{1}{\overset{2}{\int }}\frac{x^2-2x+1}{x}dx$$=\underset{1}{\overset{2}{\int }}\left(x+\frac{1}{x}-2\right)dx$$={\left.\left(\frac{x^2}{2}+\ln \left|x\right|-2x\right)\right|}_1^2$

$=-2+\ln 2+\frac{3}{2}-\ln 1=\ln 2-\frac{1}{2}$

c) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(3\sin x-2\right)dx$$=3\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sin xdx-2\underset{0}{\overset{\frac{\pi }{2}}{\int }}dx$$={\left.\left(-3\cos x-2x\right)\right|}_0^{\frac{\pi }{2}}=-\pi +3$

d) $\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{{\sin }^{2}x}{1+\cos x}dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\frac{1-{\cos }^{2}x}{1+\cos x}dx=\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left(1-\cos x\right)dx$$=\underset{0}{\overset{\frac{\pi }{2}}{\int }}dx-\underset{0}{\overset{\frac{\pi }{2}}{\int }}\cos xdx$

$={\left.\left(x-\sin x\right)\right|}_0^{\frac{\pi }{2}}=\frac{\pi }{2}-1$

Bài 4 trang 20 Toán 12 Tập 2: Tính các tích phân sau:

a) $\underset{-2}{\overset{1}{\int }}\left|2x+2\right|dx$;               b) $\underset{0}{\overset{4}{\int }}\left|x^2-4\right|dx$;                c) $\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left|\sin x\right|dx$

Lời giải:

a) $\underset{-2}{\overset{1}{\int }}\left|2x+2\right|dx$$=\underset{-2}{\overset{-1}{\int }}\left|2x+2\right|dx+\underset{-1}{\overset{1}{\int }}\left|2x+2\right|dx$$=-2\underset{-2}{\overset{-1}{\int }}\left(x+1\right)dx+2\underset{-1}{\overset{1}{\int }}\left(x+1\right)dx$

$={\left.-\left(x^2+2x\right)\right|}_{-2}^{-1}+{\left.\left(x^2+2x\right)\right|}_{-1}^1$$=1+3+1=5$

b) $\underset{0}{\overset{4}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left|x^2-4\right|dx+\underset{2}{\overset{4}{\int }}\left|x^2-4\right|dx$$=\underset{0}{\overset{2}{\int }}\left(4-x^2\right)dx+\underset{2}{\overset{4}{\int }}\left(x^2-4\right)dx$

$={\left.\left(4x-\frac{x^3}{3}\right)\right|}_0^2+{\left.\left(\frac{x^3}{3}-4x\right)\right|}_2^4$$=\frac{16}{3}+\frac{16}{3}+\frac{16}{3}=16$

c) $\underset{-\frac{\pi }{2}}{\overset{\frac{\pi }{2}}{\int }}\left|\sin x\right|dx$$=\underset{-\frac{\pi }{2}}{\overset{0}{\int }}\left|\sin x\right|dx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\left|\sin x\right|dx$$=-\underset{-\frac{\pi }{2}}{\overset{0}{\int }}\sin xdx+\underset{0}{\overset{\frac{\pi }{2}}{\int }}\sin xdx$

$={\left.\cos x\right|}_{-\frac{\pi }{2}}^0-{\left.\cos x\right|}_0^{\frac{\pi }{2}}$$=1+1=2$

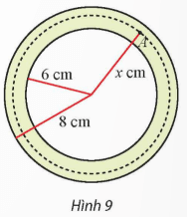
Bài 5 trang 20 Toán 12 Tập 2: Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như Hình 9. Khí bên trong ống được duy trì ở 150°C. Biết rằng nhiệt độ T(°C) tại điểm A trên thành ống là hàm số của khoảng cách x (cm) từ A đến tâm của mặt cắt và $T^{\text{'}}\left(x\right)=-\frac{30}{x}\left(6\le x\le 8\right)$.

(Nguồn: Y.A.Cengel, A.I.Gahjar, Heat and Mass Transfer, McGraw Hill, 2015)

Tìm nhiệt độ mặt ngoài của ống.

Lời giải:

Nhiệt độ tại điểm A trên thành ống là

$T\left(x\right)=\int -\frac{30}{x}dx=-30\ln \left|x\right|+C$.

Vì T(6) = 150°C nên −30ln6 + C = 150 => C = 150 + 30ln6.

Do đó T(x) = −30ln|x| + 150 + 30ln6.

Nhiệt độ ngoài mặt ống là T(8) = −30ln8 + 150 + 30ln6 ≈ 141,37°C.

Bài 6 trang 20 Toán 12 Tập 2: Giả sử tốc độ v (m/s) của một thang máy di chuyển từ tầng 1 lên tầng cao nhất theo thời gian t (giây) được cho bởi công thức: $v\left(t\right)=\left\{\begin{array}{l}t,0\le t\le \mathrm{2,}\\ \mathrm{2,}2<t\le \mathrm{20,}\\ 12-\mathrm{0,5}t,20<t\le 24.\end{array}\right.$

Tính quãng đường chuyển động và tốc độ trung bình của thang máy.

Lời giải:

Quãng đường chuyển động của thang máy là:

$s=\underset{0}{\overset{24}{\int }}v\left(t\right)dt$$=\underset{0}{\overset{2}{\int }}tdt+2\underset{2}{\overset{20}{\int }}dt+\underset{20}{\overset{24}{\int }}\left(12-\mathrm{0,5}t\right)dt$

$={\left.\frac{t^2}{2}\right|}_0^2+{\left.\left(2t\right)\right|}_2^{20}+{\left.\left(12t-\frac{1}{4}{t}^2\right)\right|}_{20}^{24}$

$=2+40-4+144-140$= 42 m.

Tốc độ trung bình của thang máy là: $v_{tb}=\frac{s}{24}=\frac{42}{24}=\mathrm{1,75}$(m/s).

Lời giải bài tập Toán 12 Bài 2: Tích phân hay khác:

• Giải Toán 12 trang 12
• Giải Toán 12 trang 16
• Giải Toán 12 trang 17
• Giải Toán 12 trang 18
• Giải Toán 12 trang 19