Mở đầu trang 33 Toán 12 Tập 1 - Kết nối tri thức
Một đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu để doanh thu từ tiền bán vé là lớn nhất?
Giải Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn - Kết nối tri thức
Mở đầu trang 33 Toán 12 Tập 1: Một đội bóng đá thi đấu trong một sân vận động có sức chứa 55 000 khán giả. Với giá mỗi vé là 100 nghìn đồng, số khán giả trung bình là 27 000 người. Qua thăm dò dư luận, người ta thấy rằng mỗi khi giá vé giảm thêm 10 nghìn đồng, sẽ có thêm khoảng 3000 khán giả. Hỏi ban tổ chức nên đặt giá vé là bao nhiêu để doanh thu từ tiền bán vé là lớn nhất?
Lời giải:
Gọi x (x > 0) là số lần giảm giá vé. Khi đó giá vé sau khi giảm là 100 – 10x (nghìn đồng).
Sau mỗi lần giảm giá thì có thêm 3000x khán giả.
Do đó tổng số khán giả đến xem là 27000 + 3000x.
Vì sân vận động có sức chứa 55 000 khán giá nên 27000 + 3000x ≤ 55 000
Doanh thu từ tiền bán vé là:
y = (27000 + 3000x).(100 – 10x) = −30 000x2 + 30 000x + 2 700 000.
Yêu cầu bài toán trở thành tìm giá trị lớn nhất của hàm số
y = −30 000x2 + 30 000x + 2 700 000, x > 0.
Tập xác định D = (0; +∞).
Có y' = −60 000x + 30 000; y' = 0 .
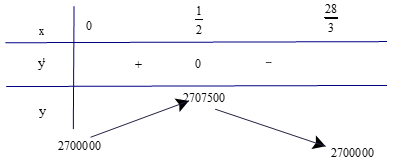
Bảng biến thiên
Dựa vào bảng biến thiên, ta thấy ban tổ chức nên đặt giá vé là 95 nghìn đồng thì doanh thu tiền bán vé là lớn nhất.
Lời giải bài tập Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn hay, chi tiết khác: