Giải Toán 12 trang 18 Tập 1 Kết nối tri thức

---

Với Giải Toán 12 trang 18 Tập 1 trong Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số Toán 12 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 12 trang 18.

Giải Toán 12 trang 18 Tập 1 Kết nối tri thức

Luyện tập 2 trang 18 Toán 12 Tập 1: Tìm giá trị lớn nhất và giá trị nhỏ nhất của các hàm số sau:

a) y = 2x³ – 3x² + 5x + 2 trên đoạn [0; 2];

b) y = (x + 1)e^−x trên đoạn [−1;1].

Lời giải:

a) Ta có y' = 6x² – 6x + 5 = 6(x² – x) + 5 = $6{\left(x-\frac{1}{2}\right)}^2+\frac{7}{2}>0$.

Hàm số luôn đồng biến.

Có y(0) = 2; y(2) = 16.

Vậy $\underset{\left[0;2\right]}{\min }y=y\left(0\right)=2;\underset{\left[0;2\right]}{\max }y=y\left(2\right)=16$.

b) Có y' = e^−x − (x + 1)e^−x; y' = 0 ⇔ e^−x − (x + 1)e^−x = 0 ⇔ x + 1 = 1 ⇔ x = 0.

Có y(−1) = 0; y(0) = 1; y(1) = $\frac{2}{e}$.

Vậy $\underset{\left[-1;1\right]}{\min }y=y(-1)=0;\underset{\left[-1;1\right]}{\max }y=y\left(0\right)=1$.

Vận dụng trang 18 Toán 12 Tập 1: Giả sử sự lây lan của một loại virus ở một địa phương có thể được mô hình hóa bằng hàm số N(t) = −t³ + 12t², 0 £ t £ 12, trong đó N là số người bị nhiễm bệnh (tính bằng trăm người) và t là thời gian (tuần).

Lời giải:

a) Có N'(t) = −3t² + 24t; N'(t) = 0 ⇔ t = 0 hoặc t = 8.

Có N(0) = 0; N(8) = 256; N(12) = 0.

Vậy giá trị lớn nhất của hàm số là N(8) = 256.

Vậy số người tối đa bị nhiễm ở địa phương đó là 256 người.

b) Có N'(t) = −3t² + 24t.

Để xác định thời điểm virus lây nhanh nhất, ta sẽ đi tìm điểm cực đại của N'(t).

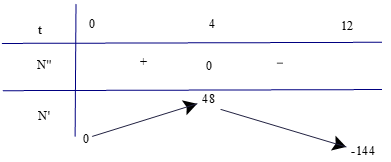
Có N"(t) = −6t + 24; N"(t) = 0 ⇔ t = 4.

Lập bảng biến thiên

Dựa vào bảng biến thiên, ta có virus lây lan nhanh nhất vào thời điểm t = 4 tuần.

Lời giải bài tập Toán 12 Bài 2: Giá trị lớn nhất và giá trị nhỏ nhất của hàm số hay khác:

• Giải Toán 12 trang 15
• Giải Toán 12 trang 17
• Giải Toán 12 trang 19