Bài 6 trang 118 Toán 7 Tập 2 Cánh diều
Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
Giải Toán 7 Bài 13: Tính chất ba đường cao của tam giác - Cánh diều
Bài 6 trang 118 Toán lớp 7 Tập 2: Cho tam giác ABC có G là trọng tâm, H là trực tâm, I là giao điểm của ba đường phân giác, O là giao điểm của ba đường trung trực. Chứng minh rằng:
a) Nếu tam giác ABC đều thì bốn điểm G, H, I, O trùng nhau;
b) Nếu tam giác ABC có hai điểm H, I trùng nhau thì tam giác ABC là tam giác đều.
Lời giải:
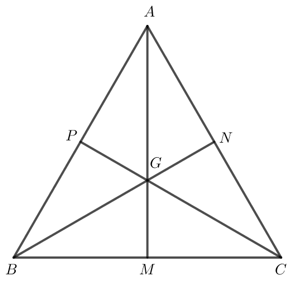
a)
Gọi M, N, P lần lượt là trung điểm của các cạnh BC, CA, AB.
Do tam giác ABC đều nên AB = BC = CA và .
Do M là trung điểm của BC nên BM = CM.
Xét ∆AMB và ∆AMC có:
AB = AC (chứng minh trên).
(chứng minh trên).
BM = CM (chứng minh trên).
Do đó ∆AMB = ∆AMC (c - g - c).
Suy ra (2 góc tương ứng) và (2 góc tương ứng).
Do , mà nên .
Khi đó AM vuông góc với BC tại trung điểm M của BC nên AM là đường trung trực của đoạn thẳng BC.
Lại có nên AM là đường phân giác của .
Thực hiện tương tự ta chứng minh được BN là đường trung trực của đoạn thẳng CA và BN là đường phân giác của .
CP là đường trung trực của đoạn thẳng AB và CP là đường phân giác của .
Mà AM, BN, CP cắt nhau tại G nên G, H, I, O trùng nhau.
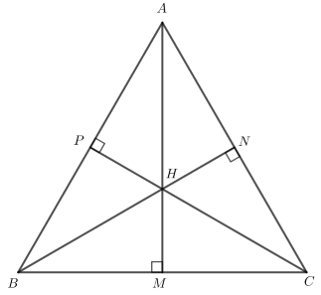
b)
Gọi M, N, P lần lượt là chân đường cao kẻ từ H đến BC, CA, AB.
Khi đó HN ⊥ AC.
Mà H là trực tâm của ∆ABC nên BH ⊥ AC.
HN ⊥ AC, BH ⊥ AC nên B, H, N thẳng hàng.
Xét ∆APH vuông tại P và ∆CMH vuông tại M có:
(2 góc đối đỉnh).
HP = HM (theo giả thiết).
Do đó ∆APH = ∆CMH (góc nhọn - cạnh góc vuông).
Suy ra HA = HC (2 cạnh tương ứng).
Xét ∆HNA vuông tại N và ∆HNC vuông tại N có:
HN chung.
HA = HC (chứng minh trên).
Do đó ∆HNA = ∆HNC (2 cạnh góc vuông).
Suy ra AN = CN (2 cạnh tương ứng).
Khi đó N là trung điểm của AC.
HN ⊥ AC tại trung điểm N của AC nên HN là đường trung trực của đoạn thẳng AC.
Mà B, H, N thẳng hàng nên B thuộc đường trung trực của đoạn thẳng AC.
Do đó BA = BC.
Thực hiện tương tự, ta chứng minh được CA = CB.
Do đó AB = BC = CA.
Vậy tam giác ABC đều.
Lời giải bài tập Toán 7 Bài 13: Tính chất ba đường cao của tam giác hay, chi tiết khác: