Luyện tập 3 trang 118 Toán 7 Tập 2 Cánh diều
Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
Giải Toán 7 Bài 13: Tính chất ba đường cao của tam giác - Cánh diều
Luyện tập 3 trang 118 Toán lớp 7 Tập 2: Cho tam giác ABC có trực tâm H cũng là trọng tâm của tam giác. Chứng minh tam giác ABC đều.
Lời giải:
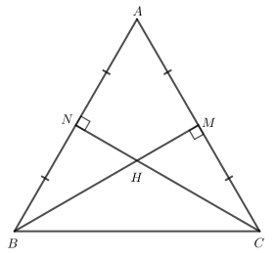
Gọi M, N lần lượt là trung điểm của AC và AB.
Do H là trực tâm của tam giác ABC nên CH ⊥ AB, BH ⊥ AC hay CN ⊥ AB, BM ⊥ AC.
Lại có H là trọng tâm của tam giác ABC nên BM, CN là các đường trung tuyến của tam giác ABC.
Khi đó BM vuông góc với AC tại trung điểm M của AC nên BM là đường trung trực của đoạn thẳng AC.
Do đó BA = BC (1).
Do CN vuông góc với AB tại trung điểm N của AB nên CN là đường trung trực của đoạn thẳng AB.
Do đó CA = CB (2).
Từ (1) và (2) suy ra AB = BC = CA nên tam giác ABC đều.
Lời giải bài tập Toán 7 Bài 13: Tính chất ba đường cao của tam giác hay, chi tiết khác: