Giải Toán 7 trang 35 Tập 1 Cánh diều

---

Haylamdo biên soạn và sưu tầm giải Toán 7 trang 35 Tập 1 trong Bài 1. Số vô tỉ. Căn bậc hai số học Toán 7 Tập 1 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 35.

Giải Toán 7 trang 35 Tập 1 Cánh diều

Bài 1 trang 35 Toán lớp 7 Tập 1:

a) Đọc các số sau: $\sqrt{15};\sqrt{\mathrm{27,6}};\sqrt{\mathrm{0,82}}$.

b) Viết các số sau: Căn bậc hai số học của 39; căn bậc hai số học của $\frac{9}{11}$; căn bậc hai số học của $\frac{89}{27}$.

Lời giải:

a) Đọc số:

$\sqrt{15}$: Căn bậc hai số học của mười lăm.

$\sqrt{27,6}$: Căn bậc hai số học của hai mươi bảy phẩy sáu.

$\sqrt{0,82}$: Căn bậc hai số học của không phẩy tám mươi hai.

b) 

Căn bậc hai số học của 39 là $\sqrt{39}$.

Căn bậc hai số học của $\frac{9}{11}$ là $\sqrt{\frac{9}{11}}$

Căn bậc hai số học của $\frac{89}{27}$ là $\sqrt{\frac{89}{27}}$

Bài 2 trang 35 Toán lớp 7 Tập 1: Chứng tỏ rằng:

a) Số 0,8 là căn bậc hai số học của số 0,64; 

b) Số –11 không phải căn bậc hai số học của số 121.

c) Số 1,4 là căn bậc hai số học của số 1,96 nhưng số –1,4 không phải căn bậc hai số học của số 1,96.

Lời giải:

a) Ta có: (0,8)² = 0,8.0,8 = 0,64 và 0,8 > 0 nên số 0,8 là căn bậc hai số học của số 0,64.

b) Ta có: (–11)² = (–11).(–11) = 121 nhưng –11 < 0 nên số –11 không là căn bậc hai số học của số 121.

c) Ta có: (1,4)² = 1,4.1,4 = 1,96 và 1,4 > 0 nên số 1,4 là căn bậc hai số học của số 1,96.

(–1,4)² = (–1,4).(–1,4) = 1,96 nhưng –1,4 < 0 nên số –1,4 không là căn bậc hai số học của số 1,96.

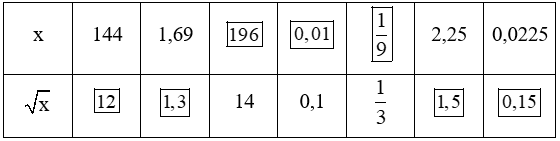
Bài 3 trang 35 Toán lớp 7 Tập 1: Tìm số thích hợp cho $\boxed{?}$:

Lời giải:

+) Ta có: 144 = 12² và 12 > 0 nên $\sqrt{x}=\sqrt{144}$=12. 

Khi đó $\boxed{?}$ điền số 12.

+) Ta có: 1,69 = 1,3² và 1,3 > 0 nên  $\sqrt{x}=\sqrt{\mathrm{1,69}}$= 1,3. 

Khi đó $\boxed{?}$ điền số 1,3.

+) Ta có: 14² = 14.14 = 196 nên x = 196. 

Khi đó $\boxed{?}$ điền số 196.

+) Ta có: 0,1² = 0,1.0,1 = 0,01 nên x = 0,01. 

Khi đó $\boxed{?}$ điền số 0,01.

+) Ta có: ${\left(\frac{1}{3}\right)}^2=\frac{1}{3}.\frac{1}{3}=\frac{1}{9}$ nên x = $\frac{1}{9}$. 

Khi đó $\boxed{?}$ điền số $\frac{1}{9}$.

+) Ta có: 2,25 = 1,5² và 1,5 > 0 nên $\sqrt{x}=\sqrt{\mathrm{2,25}}=\mathrm{1,5}$. 

Khi đó $\boxed{?}$ điền số 1,5.

+) Ta có: 0,0225 = 0,15² và 0,15 > 0 nên $\sqrt{x}=\sqrt{\mathrm{0,0225}}=\mathrm{0,15}$.

Khi đó $\boxed{?}$ điền số 0,15.

Ta có bảng sau: 

Bài 4 trang 35 Toán lớp 7 Tập 1: Tính giá trị của biểu thức: 

a) $\sqrt{\mathrm{0,49}}+\sqrt{\mathrm{0,64}}$;

b) $\sqrt{\mathrm{0,36}}-\sqrt{\mathrm{0,81}}$;

c) $8.\sqrt{9}-\sqrt{64}$

d) $0,1.\sqrt{400}+\mathrm{0,2.}\sqrt{1600}$ 

Lời giải:

a)$\sqrt{\mathrm{0,49}}+\sqrt{\mathrm{0,64}}=\sqrt{{\mathrm{0,7}}^2}+\sqrt{{\mathrm{0,8}}^2}=\mathrm{0,7}+\mathrm{0,8}=\mathrm{1,5}$.

b) $\sqrt{\mathrm{0,36}}-\sqrt{\mathrm{0,81}}=\sqrt{{\mathrm{0,6}}^2}-\sqrt{{\mathrm{0,9}}^2}=\mathrm{0,6}-\mathrm{0,9}=-\mathrm{0,3}$

c) $8.\sqrt{9}-\sqrt{64}=8.\sqrt{3^2}-\sqrt{8^2}=8.3-8=24-8=16$

d)  $0,1.\sqrt{400}+\mathrm{0,2.}\sqrt{1600}=\mathrm{0,1.}\sqrt{{20}^2}+\mathrm{0,2.}\sqrt{{40}^2}=\mathrm{0,1.20}+\mathrm{0,2.40}=2+8=10$

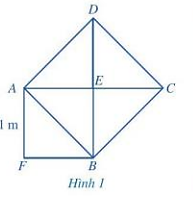
Bài 5 trang 35 Toán lớp 7 Tập 1: Quan sát Hình 1, ở đó hình vuông AEBF có cạnh bằng 1 dm, hình vuông ABCD có cạnh AB là một đường chéo của hình vuông AEBF.

a) Tính diện tích của hình vuông ABCD.

b) Tính độ dài đường chéo AB.

 

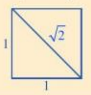
Lưu ý: $\sqrt{2}$ là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1.

Lời giải:

a) Quan sát Hình 1 ta thấy hình vuông ABCD được tạo thành từ 4 tam giác nhỏ bằng nhau nên diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB. 

Hình vuông AEBF là hình vuông có cạnh bằng 1 và tạo bởi hai tam giác là AEB và AFB nên diện tích của hình vuông AEBF gấp 2 lần diện tích của tam giác AEB.

Diện tích hình vuông AEBF có cạnh bằng 1 m là: 1.1 = 1 (dm²).

Diện tích hình vuông AEBF gấp 2 lần diện tích tam giác AEB nên diện tích tam giác AEB là: 1 : 2 =  $\frac{1}{2}$(dm²).

Diện tích hình vuông ABCD gấp 4 lần diện tích tam giác AEB nên diện tích hình vuông ABCD là: $\frac{1}{2}.4=2$(dm²).

Vậy diện tích hình vuông ABCD là 2 dm².

b) Do $\sqrt{2}$ là độ dài đường chéo của hình vuông có độ dài cạnh bằng 1, mà hình vuông AEBF có cạnh bằng 1 dm nên đường chéo AB là $\sqrt{2}$dm.

Vậy độ dài đường chéo AB là $\sqrt{2}$dm.

Lời giải bài tập Toán lớp 7 Bài 1. Số vô tỉ. Căn bậc hai số học Cánh diều hay khác:

• Giải Toán 7 trang 33 Tập 1
• Giải Toán 7 trang 34 Tập 1