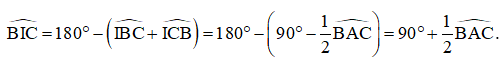Giải Toán 7 trang 111 Tập 2 Cánh diều
Haylamdo biên soạn và sưu tầm giải Toán 7 trang 111 Tập 2 trong Bài 11: Tính chất ba đường phân giác của tam giác Toán 7 Tập 2 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 111.
Giải Toán 7 trang 111 Tập 2 Cánh diều
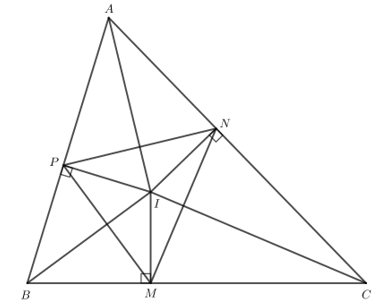
Luyện tập 3 trang 111 Toán lớp 7 Tập 2: Cho tam giác ABC có I là giao điểm của ba đường phân giác. M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB. Chứng minh rằng: IA, IB, IC lần lượt là đường trung trực của các đoạn thẳng NP, PM, MN.
Lời giải:
+) Chứng minh IA là đường trung trực của NP.
Do IP = IN nên I thuộc đường trung trực của NP.
Xét ∆AIP vuông tại P và ∆AIN vuông tại N có:
AI chung.
IP = IN (theo giả thiết).
Do đó ∆AIP = ∆AIN (cạnh huyền - cạnh góc vuông).
Suy ra AP = AN (2 cạnh tương ứng).
Do AP = AN nên A thuộc đường trung trực của NP.
Do đó IA là đường trung trực của NP.
+) Chứng minh IB là đường trung trực của PM.
Do IP = IM nên I thuộc đường trung trực của PM.
Xét ∆BIP vuông tại P và ∆BIM vuông tại M có:
BI chung.
IP = IM (theo giả thiết).
Do đó ∆BIP = ∆BIM (cạnh huyền - cạnh góc vuông).
Suy ra BP = BM (2 cạnh tương ứng).
Do BP = BM nên B thuộc đường trung trực của PM.
Do đó IB là đường trung trực của PM.
+) Chứng minh IC là đường trung trực của MN.
Do IM = IN nên I thuộc đường trung trực của MN.
Xét ∆CIM vuông tại M và ∆CIN vuông tại N có:
CI chung.
IM = IN (theo giả thiết).
Do đó ∆CIM = ∆CIN (cạnh huyền - cạnh góc vuông).
Suy ra CM = CN (2 cạnh tương ứng).
Do CM = CN nên C thuộc đường trung trực của MN.
Do đó IC là đường trung trực của MN.
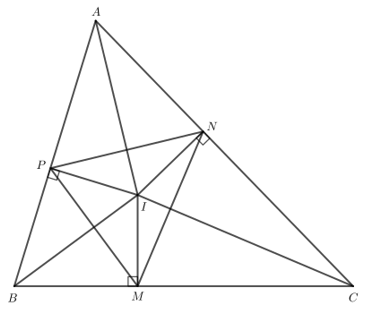
Bài 1 trang 111 Toán lớp 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I. Gọi M, N, P lần lượt là hình chiếu của I trên các cạnh BC, CA, AB.
a) Các tam giác IMN, INP, IPM có là tam giác cân không? Vì sao?
b) Các tam giác ANP, BPM, CMN có là tam giác cân không? Vì sao?
Lời giải:
a) Tam giác ABC có I là giao điểm ba đường phân giác nên I cách đều 3 cạnh của tam giác ABC.
Do đó IM = IN = IP.
Do IM = IN nên tam giác IMN cân tại I.
Do IN = IP nên tam giác INP cân tại I.
Do IP = IM nên tam giác IPM cân tại I.
b) Xét ∆AIP vuông tại P và ∆AIN vuông tại N có:
AI chung.
IP = IN (theo giả thiết).
Do đó ∆AIP = ∆AIN (cạnh huyền - cạnh góc vuông).
Suy ra AP = AN (2 cạnh tương ứng).
Tam giác ANP có AP = AN nên tam giác ANP cân tại A.
Xét ∆BIP vuông tại P và BIM vuông tại M có:
BI chung.
IP = IM (theo giả thiết).
Do đó ∆BIP = ∆BIM (cạnh huyền - cạnh góc vuông).
Suy ra BP = BM (2 cạnh tương ứng).
Tam giác BPM có BP = BM nên tam giác BPM cân tại B.
Xét ∆CIM vuông tại M và ∆CIN vuông tại N có:
CI chung.
IM = IN (theo giả thiết).
Do đó ∆CIM = ∆CIN (cạnh huyền - cạnh góc vuông).
Suy ra CM = CN (2 cạnh tương ứng).
Tam giác CMN có CM = CN nên tam giác CMN cân tại C.
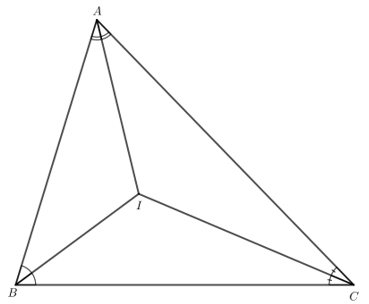
Bài 2 trang 111 Toán lớp 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I. Chứng minh:
a) ;
b) .
Lời giải:
a) Do AI là đường phân giác của nên .
Do BI là đường phân giác của nên .
Do CI là đường phân giác của nên
Suy ra
.
Trong tam giác ABC, ta có nên
.
b) Do CI là đường phân giác của nên .
Suy ra .
Do đó
.
Trong tam giác BIC: nên
Bài 3 trang 111 Toán lớp 7 Tập 2: Tam giác ABC có ba đường phân giác cắt nhau tại I và AB < AC.
a) Chứng minh ;
b) So sánh IB và IC.
Lời giải:
a) Tam giác ABC có AB < AC nên .
Do BI là đường phân giác của nên .
Do CI là đường phân giác của nên .
Do nên .
Do đó .
b) Do , mà nên .
Tam giác BIC có nên IB < IC.
Lời giải bài tập Toán lớp 7 Bài 11: Tính chất ba đường phân giác của tam giác Cánh diều hay khác: