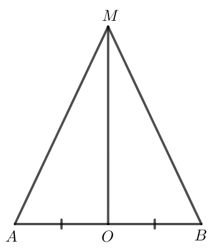
Hoạt động 3 trang 101 Toán 7 Tập 2 Cánh diều
Cho đoạn thẳng AB có trung điểm O. Giả sử M là một điểm khác O sao cho MA = MB.
Giải Toán 7 Bài 9: Đường trung trực của một đoạn thẳng - Cánh diều
Hoạt động 3 trang 101 Toán lớp 7 Tập 2: Cho đoạn thẳng AB có trung điểm O. Giả sử M là một điểm khác O sao cho MA = MB.
a) Hai tam giác MOA và MOB có bằng nhau hay không? Vì sao?
b) Đường thẳng MO có là đường trung trực của đoạn thẳng AB hay không? Vì sao?
Lời giải:
a) Xét ∆MOA và ∆MOB có:
MO chung.
OA = OB (theo giả thiết).
MA = MB (theo giả thiết).
Do đó ∆MOA = ∆MOB (c - c - c).
b) Do ∆MOA = ∆MOB (c - c - c) nên OA = OB (2 cạnh tương ứng) và (2 góc tương ứng).
Do OA = OB và O nằm giữa A và B nên O là trung điểm của AB.
Do mà nên .
Do đó MO ⊥ AB.
Khi đó MO vuông góc với AB tại trung điểm O của AB.
Vậy MO là đường trung trực của đoạn thẳng AB.
Lời giải bài tập Toán 7 Bài 9: Đường trung trực của một đoạn thẳng hay, chi tiết khác: