Bài 2 trang 86 Toán 7 Tập 1 Chân trời sáng tạo

❮ Bài trước Bài sau ❯

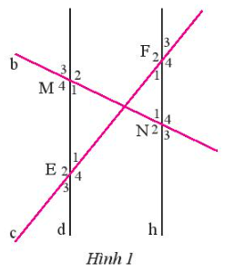
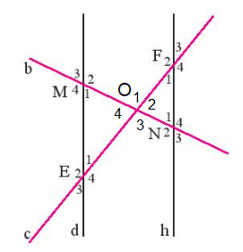
Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1.

Giải Toán 7 Bài tập cuối chương 4 - Chân trời sáng tạo

Bài 2 trang 86 Toán 7 Tập 1: Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1.

Lời giải:

Bài 2 trang 86 Toán 7 Tập 1 Chân trời sáng tạo

Gọi O là giao điểm của hai đường thẳng b và c.

Ta có: ${\hat{O}}_{1} = {\hat{O}}_{3}$ ; ${\hat{O}}_{2} = {\hat{O}}_{4}$ (các góc đối đỉnh);

${\hat{M}}_{1} = {\hat{M}}_{3}$ ; ${\hat{M}}_{2} = {\hat{M}}_{4}$ (các góc đối đỉnh);

${\hat{E}}_{1} = {\hat{E}}_{3}$ ; ${\hat{E}}_{2} = {\hat{E}}_{4}$ (các góc đối đỉnh);

${\hat{N}}_{1} = {\hat{N}}_{3}$ ; ${\hat{N}}_{2} = {\hat{N}}_{4}$ (các góc đối đỉnh);

${\hat{F}}_{1} = {\hat{F}}_{3}$ ; ${\hat{F}}_{2} = {\hat{F}}_{4}$ (các góc đối đỉnh).

Vì d // h nên ta có các cặp góc so le trong bằng nhau và các cặp góc đồng vị bằng nhau.

- Các cặp góc so le trong: ${\hat{M}}_{1} = {\hat{N}}_{1}$ ; ${\hat{M}}_{2} = {\hat{N}}_{2}$ ; ${\hat{E}}_{1} = {\hat{F}}_{1}$ ; ${\hat{E}}_{4} = {\hat{F}}_{2}$ .

- Các cặp góc đồng vị: ${\hat{M}}_{1} = {\hat{N}}_{3}$ ; ${\hat{M}}_{2} = {\hat{N}}_{4}$ ; ${\hat{M}}_{3} = {\hat{N}}_{1}$ ; ${\hat{M}}_{4} = {\hat{N}}_{2}$ ; ${\hat{E}}_{1} = {\hat{F}}_{3}$ ; ${\hat{E}}_{2} = {\hat{F}}_{2}$ ; ${\hat{E}}_{3} = {\hat{F}}_{1}$ ; ${\hat{E}}_{4} = {\hat{F}}_{4}$ .

Vậy cặp góc bằng nhau có trong Hình 1 là:

${\hat{O}}_{1} = {\hat{O}}_{3}; {\hat{O}}_{2} = {\hat{O}}_{4}; {\hat{M}}_{1} = {\hat{M}}_{3}; {\hat{M}}_{2} = {\hat{M}}_{4}; {\hat{E}}_{1} = {\hat{E}}_{3}; {\hat{E}}_{2} = {\hat{E}}_{4}; {\hat{N}}_{1} = {\hat{N}}_{3}; {\hat{N}}_{2} = {\hat{N}}_{4}; {\hat{F}}_{1} = {\hat{F}}_{3}; {\hat{F}}_{2} = {\hat{F}}_{4}; {\hat{M}}_{1} = {\hat{N}}_{1}; {\hat{M}}_{2} = {\hat{N}}_{2}; {\hat{E}}_{1} = {\hat{F}}_{1}; {\hat{E}}_{4} = {\hat{F}}_{4}; {\hat{M}}_{1} = {\hat{N}}_{3}; {\hat{M}}_{2} = {\hat{N}}_{4}; {\hat{M}}_{3} = {\hat{N}}_{1}; {\hat{M}}_{4} = {\hat{N}}_{2}; {\hat{E}}_{1} = {\hat{F}}_{3}; {\hat{E}}_{2} = {\hat{F}}_{4}; {\hat{E}}_{3} = {\hat{F}}_{1}; {\hat{E}}_{4} = {\hat{F}}_{1}$ .

Lời giải bài tập Toán 7 Bài tập cuối chương 4 hay, chi tiết khác:

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác:

❮ Bài trước Bài sau ❯

Giải Toán lớp 7 Chân trời sáng tạo

Bài 2 trang 86 Toán 7 Tập 1 Chân trời sáng tạo

Giải Toán 7 Bài tập cuối chương 4 - Chân trời sáng tạo

Xem thêm lời giải bài tập Toán lớp 7 Chân trời sáng tạo hay, chi tiết khác: