Bài 4 trang 66 Toán 7 Tập 2 Chân trời sáng tạo
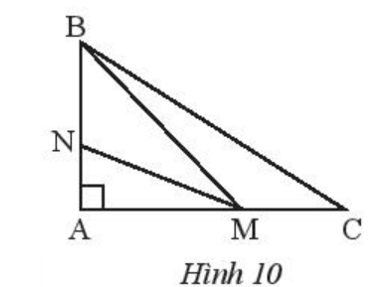
Quan sát Hình 10.
Giải Toán 7 Bài 4: Đường vuông góc và đường xiên - Chân trời sáng tạo
Bài 4 trang 66 Toán 7 Tập 2: Quan sát Hình 10.
a) Tìm đoạn ngắn nhất trong các đoạn BA, BM, BC.
b) Tìm đoạn ngắn nhất trong các đoạn MA, MN, MB.
c) Chứng minh rằng MA < BC.
Lời giải:
a) Ta thấy BA là đường vuông góc kẻ từ B đến AC.
BM và BC là đường xiên kẻ từ B đến AC.
Do đó BA là đoạn ngắn nhất trong các đoạn BA, BM, BC.
b) Ta thấy MA là đường vuông góc kẻ từ M đến AB.
MN và MB là đường xiên kẻ từ M đến AB.
Do đó MA là đoạn ngắn nhất trong các đoạn MA, MN, MB.
c) Ta có MA < MB (1).
(2 góc kề bù) nên .
(tổng 3 góc trong tam giác ABM) nên
.
Do đó .
Khi đó là góc tù.
Tam giác BMC có là góc tù nên là góc lớn nhất trong tam giác BMC.
Khi đó BC là cạnh lớn nhất trong tam giác BMC.
Do đó BM < BC (2).
Từ (1) và (2) ta có MA < MB < BC nên MA < BC.
Lời giải bài tập Toán 7 Bài 4: Đường vuông góc và đường xiên hay, chi tiết khác: