Bài 4 trang 82 Toán 7 Tập 2 Chân trời sáng tạo
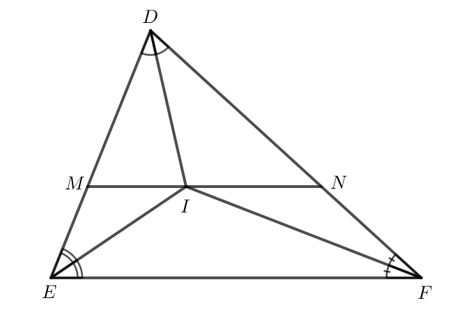
Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.
Giải Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác - Chân trời sáng tạo
Bài 4 trang 82 Toán 7 Tập 2: Cho tam giác DEF. Tia phân giác của góc D và E cắt nhau tại I. Qua I kẻ đường thẳng song song với EF, đường thẳng này cắt DE tại M, cắt DF tại N. Chứng minh rằng ME + NF = MN.
Lời giải:
Tam giác DEF có I là giao điểm hai đường phân giác.
Mà ba đường phân giác của tam giác DEF đồng quy nên IF là đường phân giác của .
EI là đường phân giác của nên .
Do IM // EF nên (2 góc so le trong).
Suy ra .
Tam giác MIE có nên tam giác MIE cân tại M.
Do đó ME = MI (1).
FI là đường phân giác của nên .
Do IN // EF nên (2 góc so le trong).
Suy ra .
Tam giác NIF có nên tam giác NIF cân tại N.
Do đó NI = NF (2).
Từ (1) và (2) ta có ME + NF = MI + NI = MN.
Vậy ME + NF = MN.
Lời giải bài tập Toán 7 Bài 9: Tính chất ba đường phân giác của tam giác hay, chi tiết khác: