Giải Toán 7 trang 80 Tập 1 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 80 Tập 1 trong Bài 3: Hai đường thẳng song song Toán lớp 7 Tập 1 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 80.

Giải Toán 7 trang 80 Tập 1 Chân trời sáng tạo

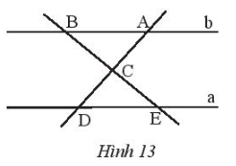
Vận dụng 1 trang 80 Toán 7 Tập 1: Tìm các cặp góc bằng nhau của hai tam giác ABC và DEC trong Hình 13, biết a // b.

Lời giải:

Vì a // b nên ta có các cặp góc bằng nhau của hai tam giác ABC và DEC là:

$\widehat{ABC}=\widehat{DEC}; \widehat{BAC}=\widehat{EDC}$ (các cặp góc so le trong).

Vậy các cặp góc bằng nhau của hai tam giác ABC và DEC là

$\widehat{ABC}=\widehat{DEC}; \widehat{BAC}=\widehat{EDC}$.

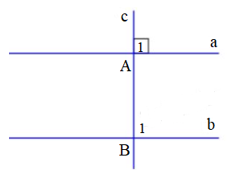
Vận dụng 2 trang 80 Toán 7 Tập 1: Cho hai đường thẳng a, b song song với nhau, đường thẳng c vuông góc với a tại A và cắt b tại B. Hãy giải thích tại sao đường thẳng c cũng vuông góc với b.

Lời giải:

Gọi giao điểm của hai đường thẳng a và b với đường thẳng c lần lượt là A và B.

Ta có $a\perp c$ tại A nên ${\widehat{A}}_1={90}^o$.

Vì a // b nên ${\widehat{A}}_1={\widehat{B}}_1={90}^o$ (hai góc đồng vị).

Do đó $c\perp b$ tại B.

Vậy đường thẳng c vuông góc với đường thẳng b.

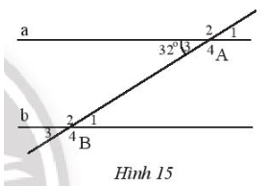
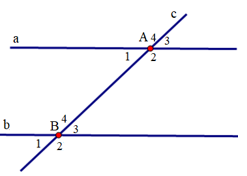
Bài 1 trang 80 Toán 7 Tập 1: Trong Hình 15, cho biết a // b. Tìm số đo các góc đỉnh A và B.

Lời giải:

Vì ${\widehat{A}}_3$ và ${\widehat{A}}_4$ là hai góc kề bù nên:

${\widehat{A}}_3+{\widehat{A}}_4={180}^o$

${32}^o+{\widehat{A}}_4={180}^o$

Suy ra ${\widehat{A}}_4={180}^o-{32}^o={148}^o$.

Ta có: ${\widehat{A}}_1={\widehat{A}}_3={32}^o$; ${\widehat{A}}_2={\widehat{A}}_4={148}^o$ (các cặp góc đối đỉnh)

Vì a // b nên ${\widehat{A}}_3={\widehat{B}}_3={32}^o$ (hai góc đồng vị).

Vì ${\widehat{B}}_3$ và ${\widehat{B}}_4$ là hai góc kề bù nên:

${\widehat{B}}_3+{\widehat{B}}_4={180}^o$

${32}^o+{\widehat{B}}_4={180}^o$

Suy ra ${\widehat{B}}_4={180}^o-{32}^o={148}^o$.

Ta có: ${\widehat{B}}_1={\widehat{B}}_3={32}^o$; ${\widehat{B}}_2={\widehat{B}}_4={148}^o$ (các cặp góc đối đỉnh).

Vậy số đo các góc đỉnh A và B là ${\widehat{A}}_1={\widehat{A}}_3={32}^o$; ${\widehat{A}}_2={\widehat{A}}_4={148}^o$; ${\widehat{B}}_1={\widehat{B}}_3={32}^o$; ${\widehat{B}}_2={\widehat{B}}_4={148}^o$.

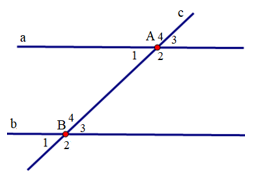
Bài 2 trang 80 Toán 7 Tập 1: Vẽ một đường thẳng cắt hai đường thẳng sao cho trong các góc tạo thành có một cặp góc so le trong bằng nhau. Đặt tên cho các góc đó.

a) Vì sao cặp góc so le trong còn lại cũng bằng nhau?

b) Vì sao các cặp góc đồng vị cũng bằng nhau?

Lời giải:

Giả sử đường thẳng c cắt hai đường thẳng a và b lần lượt tại hai điểm A và B có:

Cặp góc so le trong bằng nhau là: ${\widehat{A}}_1={\widehat{B}}_3$ (như hình vẽ).

a) Vì ${\widehat{A}}_1={\widehat{B}}_3$ mà ${\widehat{A}}_1$ và ${\widehat{B}}_3$ ở vị trí so le trong nên a // b.

Do đó: ${\widehat{A}}_2={\widehat{B}}_4$ (hai góc so le trong).

b) Vì a // b nên ta có các cặp góc đồng vị bằng nhau như sau:

${\widehat{A}}_1={\widehat{B}}_1;{\widehat{A}}_2={\widehat{B}}_2;{\widehat{A}}_3={\widehat{B}}_3;{\widehat{A}}_4={\widehat{B}}_4$.

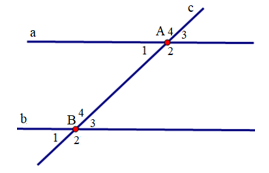
Bài 3 trang 80 Toán 7 Tập 1: Hãy nói các cách để kiểm tra hai đường thẳng song song mà em biết.

Lời giải:

Muốn kiểm tra xem hai đường thẳng a, b cho trước có song song với nhau hay không, ta vẽ đường thẳng c cắt đường thẳng a, b.

Cách 1: Đo một cặp góc so le trong, nếu chúng bằng nhau thì a // b.

Chẳng hạn: Ta đo số đo ${\widehat{A}}_1$ và ${\widehat{B}}_3$ có: ${\widehat{A}}_1={\widehat{B}}_3$.

Mà ${\widehat{A}}_1$ và ${\widehat{B}}_3$ là hai góc vị trí so le trong nên a // b.

Cách 2: Đo một cặp góc đồng vị, nếu chúng bằng nhau thì a // b.

Chẳng hạn: Ta đo số đo ${\widehat{A}}_1$ và ${\widehat{B}}_1$ có: ${\widehat{A}}_1={\widehat{B}}_1$.

Mà ${\widehat{A}}_1$ và ${\widehat{B}}_1$ là hai góc đồng vị nên a // b.

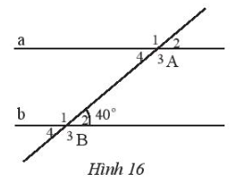
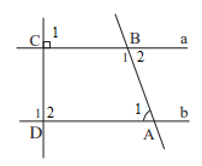
Bài 4 trang 80 Toán 7 Tập 1: Cho Hình 16, biết a // b.

a) Chỉ ra góc ở vị trí so le trong, đồng vị với góc ${\widehat{B}}_2$.

b) Tính số đo các góc ${\widehat{A}}_4,{\widehat{A}}_2,{\widehat{B}}_3$.

c) Tính số đo các góc ${\widehat{B}}_1,{\widehat{A}}_1$.

Lời giải:

a) Góc so le trong với ${\widehat{B}}_2$ là ${\widehat{A}}_4$;

Góc đồng vị với ${\widehat{B}}_2$ là ${\widehat{A}}_2$.

b) Ta có: a // b.

+ ${\widehat{A}}_4$ và ${\widehat{B}}_2$ là hai góc so le trong nên ${\widehat{A}}_4={\widehat{B}}_2={40}^o$;

+ ${\widehat{A}}_2$ và ${\widehat{B}}_2$ là hai góc đồng vị nên ${\widehat{A}}_2={\widehat{B}}_2={40}^o$.

Vì ${\widehat{B}}_2$ và ${\widehat{B}}_3$ là hai góc kề bù nên ${\widehat{B}}_2+{\widehat{B}}_3={180}^o$

${40}^o+{\widehat{B}}_3={180}^o$

Suy ra ${\widehat{B}}_3={180}^o-{40}^o={140}^o$.

Vậy số đo các góc

${\widehat{A}}_4={40}^o,{\widehat{A}}_2={40}^o,{\widehat{B}}_3={140}^o$.

c) Vì ${\widehat{B}}_1$ và ${\widehat{B}}_2$ là hai góc kề bù nên:

${\widehat{B}}_1+{\widehat{B}}_2={180}^o$

${\widehat{B}}_1+{40}^o={180}^o$

Suy ra: ${\widehat{B}}_1={180}^o-{40}^o={140}^o$.

Vì a // b nên ${\widehat{A}}_1={\widehat{B}}_1={140}^o$ (hai góc đồng vị).

Vậy ${\widehat{B}}_1={140}^o,{\widehat{A}}_1={140}^o$.

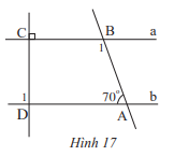
Bài 5 trang 80 Toán 7 Tập 1: Cho Hình 17, biết a // b. Tính số đo của các góc ${\widehat{B}}_1$ và ${\widehat{D}}_1$.

Lời giải:

Vì $a\perp CD$ nên ${\widehat{C}}_1={90}^o$.

Ta có a // b:

+ ${\widehat{C}}_1$ và ${\widehat{D}}_1$ là hai góc so le trong nên ${\widehat{C}}_1={\widehat{D}}_1={90}^o$;

+ ${\widehat{A}}_1={\widehat{B}}_2$ (hai góc so le trong) nên ${\widehat{B}}_2={70}^o$.

Mà ${\widehat{B}}_1$ và ${\widehat{B}}_2$ là hai góc kề bù nên:

${\widehat{B}}_1+{\widehat{B}}_2={180}^o$

${\widehat{B}}_1+{70}^o={180}^o$.

Suy ra ${\widehat{B}}_1={180}^o-{70}^o={110}^o$.

Vậy ${\widehat{B}}_1={110}^o; {\widehat{D}}_1={90}^o$.

Lời giải bài tập Toán lớp 7 Bài 3: Hai đường thẳng song song Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 76 Tập 1
• Giải Toán 7 trang 77 Tập 1
• Giải Toán 7 trang 78 Tập 1
• Giải Toán 7 trang 79 Tập 1
• Giải Toán 7 trang 81 Tập 1