Giải Toán 7 trang 58 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 58 Tập 2 trong Bài 2: Tam giác bằng nhau Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 58.

Giải Toán 7 trang 58 Tập 2 Chân trời sáng tạo

Bài 3 trang 58 Toán 7 Tập 2: Cho hai tam giác bằng nhau ABC và DEF (các đỉnh chưa viết tương ứng), trong đó $\hat{A}=\hat{E}$, $\hat{C}=\hat{D}$. Tìm các cặp cạnh bằng nhau, cặp góc tương ứng bằng nhau còn lại.

Lời giải:

Áp dụng định lí tổng ba góc trong một tam giác ta có:

Xét tam giác ABC có: $\hat{B}=180°-\hat{A}-\hat{C}$.

Xét tam giác DEF có: $\hat{F}=180°-\hat{E}-\hat{D}$.

Mà $\hat{A}=\hat{E}$và $\hat{C}=\hat{D}$nên $\hat{B}=\hat{F}$.

Do đó $△$ABC = $△$EFD.

Khi đó AB = EF (2 cạnh tương ứng), BC = FD (2 cạnh tương ứng), CA = DE (2 cạnh tương ứng).

Vậy $\hat{B}=\hat{F}$, AB = EF, BC = FD, CA = DE.

Bài 4 trang 58 Toán 7 Tập 2: Cho biết $△$MNP = $△$DEF và MN = 4 cm, MP = 5 cm, EF = 6 cm. Tìm chu vi tam giác MNP.

Lời giải:

Do $△$MNP = $△$DEF nên MN = DE (2 cạnh tương ứng) và MP = DF (2 cạnh tương ứng).

Do đó DE = 4 cm, DF = 5 cm.

Khi đó chu vi tam giác MNP là: 4 + 5 + 6 = 15 cm.

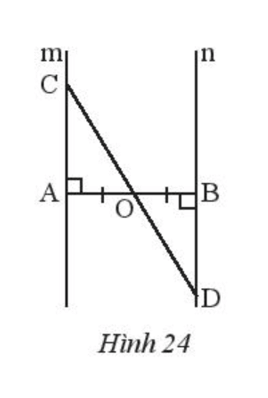
Bài 5 trang 58 Toán 7 Tập 2: Cho đoạn thẳng AB có O là trung điểm. Vẽ hai đường thẳng m và n lần lượt vuông góc với AB tại A và B. Lấy điểm C trên m, CO cắt n tại D (Hình 24). Chứng minh rằng O là trung điểm của CD.

Lời giải:

Xét tam giác OAC vuông tại A và tam giác OBD vuông tại B:

$\widehat{AOC}=\widehat{BO\text{D}}$(2 góc đối đỉnh).

OA = OB (theo giả thiết).

Do đó $△$OAC = $△$OBD (góc nhọn - cạnh góc vuông).

Suy ra OC = OD (2 cạnh tương ứng).

Mà O nằm giữa C và D nên O là trung điểm của CD.

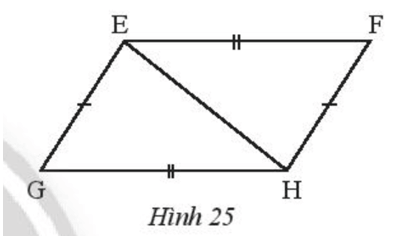
Bài 6 trang 58 Toán 7 Tập 2: Cho Hình 25 có EF = HG, EG = HF. Chứng minh rằng:

a) $△$EFH = $△$HGE.

b) EF // HG.

Lời giải:

a) Xét hai tam giác EFH và HGE có:

EF = HG (theo giả thiết).

EG = HF (theo giả thiết).

EH chung.

Do đó $△$EFH = $△$HGE (c.c.c).

b) Do DEFH = DHGE (c.c.c) nên $\widehat{F\text{E}H}=\widehat{GHE}$(2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên EF // HG.

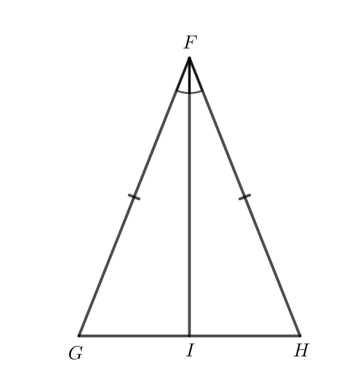
Bài 7 trang 58 Toán 7 Tập 2: Cho tam giác FGH có FG = FH. Lấy điểm I trên cạnh GH sao cho FI là tia phân giác của $\widehat{GFH}$. Chứng minh rằng hai tam giác FIG và FIH bằng nhau.

Lời giải:

Do FI là tia phân giác của $\widehat{GFH}$nên $\widehat{GFI}=\widehat{HFI}$.

Xét hai tam giác FIG và FIH có:

FG = FH (theo giả thiết).

$\widehat{GFI}=\widehat{HFI}$(chứng minh trên).

FI chung.

Do đó $△$FIG = $△$FIH (c.g.c).

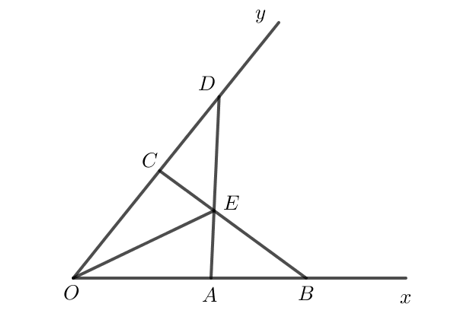
Bài 8 trang 58 Toán 7 Tập 2: Cho góc xOy. Lấy hai điểm A, B thuộc tia Ox sao cho OA < OB. Lấy hai điểm C, D thuộc tia Oy sao cho OC = OA, OD = OB. Gọi E là giao điểm của AD và BC. Chứng minh rằng:

a) AD = BC.

b) $△$EAB = $△$ECD.

c) OE là tia phân giác của góc xOy.

Lời giải:

a) Xét hai tam giác OAD và OCB có:

OA = OC (theo giả thiết).

$\hat{O}$chung.

OD = OB (theo giả thiết).

Do đó $△$OAD = $△$OCB (c.g.c).

Suy ra AD = BC (2 cạnh tương ứng).

b) Do OA = OC, OB = OD nên OB - OA = OD - OC hay AB = CD.

Do $△$OAD = $△$OCB (c.g.c) nên $\widehat{O\text{D}A}=\widehat{OBC}$(2 góc tương ứng).

$\widehat{EC\text{D}}$là góc ngoài tại đỉnh C của tam giác OBC nên $\widehat{EC\text{D}}=\widehat{COB}+\widehat{OBC}$(1).

$\widehat{EAB}$là góc ngoài tại đỉnh A của tam giác OAD nên $\widehat{EAB}=\widehat{AOD}+\widehat{ODA}$(2).

Từ (1) và (2) suy ra $\widehat{EC\text{D}}=\widehat{E\text{A}B}$.

Xét hai tam giác EAB và ECD có:

$\widehat{E\text{A}B}=\widehat{EC\text{D}}$(chứng minh trên).

AB = CD (chứng minh trên).

$\widehat{EBA}=\widehat{E\text{DC}}$(chứng minh trên).

Do đó $△$EAB = $△$ECD (g.c.g).

c) Do $△$EAB = $△$ECD (g.c.g) nên BE = DE (2 cạnh tương ứng).

Xét hai tam giác ODE và OBE có:

OD = OB (theo giả thiết).

OE chung.

DE = BE (theo giả thiết).

Do đó $△$ODE = $△$OBE (c.c.c).

Suy ra $\widehat{EOD}=\widehat{EOB}$(2 góc tương ứng).

Vậy OE là tia phân giác của $\widehat{xOy}$.

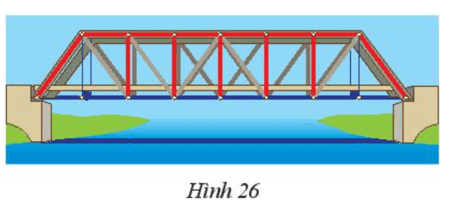
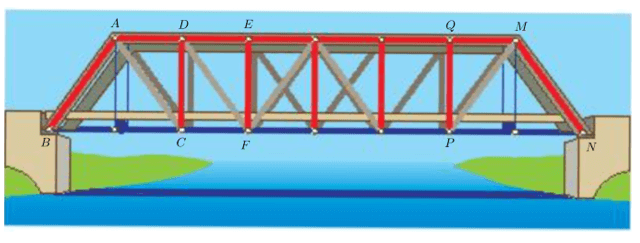
Bài 9 trang 58 Toán 7 Tập 2: Đặt tên cho một số điểm có trong Hình 26 và chỉ ra ba cặp tam giác bằng nhau trong hình đó.

Lời giải:

Đặt tên các điểm như hình trên.

Dựa vào hình trên ta có các cặp tam giác bằng nhau như sau:

$△$ABC = $△$MNP; $△$ADC = $△$MQP; $△$ADC = $△$DEF.

Lời giải bài tập Toán lớp 7 Bài 2: Tam giác bằng nhau Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 48 Tập 2

• Giải Toán 7 trang 49 Tập 2

• Giải Toán 7 trang 50 Tập 2

• Giải Toán 7 trang 51 Tập 2

• Giải Toán 7 trang 52 Tập 2

• Giải Toán 7 trang 54 Tập 2

• Giải Toán 7 trang 55 Tập 2

• Giải Toán 7 trang 56 Tập 2

• Giải Toán 7 trang 57 Tập 2