Giải Toán 7 trang 75 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 75 Tập 2 trong Bài 7: Tính chất ba đường trung tuyến của tam giác Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 75.

Giải Toán 7 trang 75 Tập 2 Chân trời sáng tạo

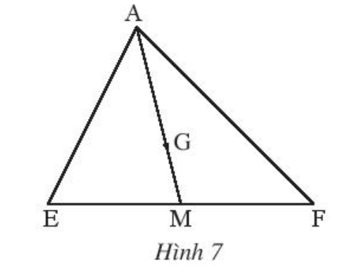
Thực hành 2 trang 75 Toán 7 Tập 2: Trong Hình 7, G là trọng tâm của tam giác AEF với đường trung tuyến AM.

Hãy tính các tỉ số:

a) $\frac{GM}{AM}$;

b) $\frac{GM}{AG}$;

c) $\frac{AG}{GM}$.

Lời giải:

a) Do G là trọng tâm của tam giác ABC nên AG = $\frac{2}{3}$AM.

Khi đó GM = AM - AG = AM - $\frac{2}{3}$AM = $\frac{1}{3}$AM.

Do đó $\frac{GM}{AM}=\frac{1}{3}$.

b) Do GM = $\frac{1}{3}$AM và AG = $\frac{2}{3}$AM nên GM : AG = $\frac{1}{3}$AM : $\frac{2}{3}$AM = $\frac{1}{2}$.

Do đó $\frac{GM}{AG}=\frac{1}{2}$.

c) Do $\frac{GM}{AG}=\frac{1}{2}$nên $\frac{AG}{GM}$= 2.

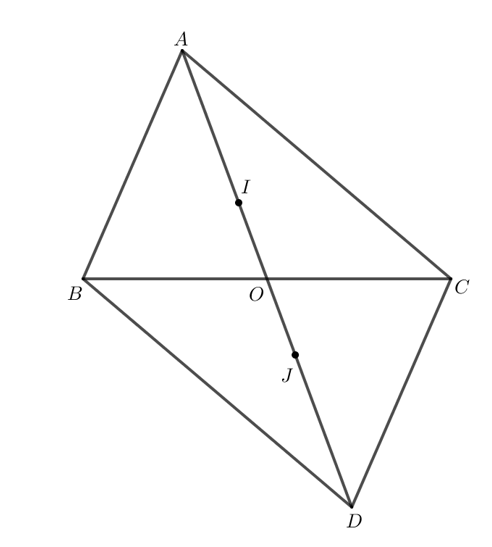
Vận dụng 2 trang 75 Toán 7 Tập 2: Cho tam giác ABC có O là trung điểm của BC, trên tia đối của tia OA, lấy điểm D sao cho OA = OD. Gọi I và J lần lượt là trọng tâm các tam giác ABC và DBC. Chứng minh rằng AI = IJ = JD.

Lời giải:

Do O là trung điểm của BC nên AO là đường trung tuyến của tam giác ABC, DO là đường trung tuyến của tam giác DBC.

Do I là trọng tâm của tam giác ABC nên I nằm trên AO sao cho AI = $\frac{2}{3}$AO.

Do J là trọng tâm của tam giác DBC nên J nằm trên DO sao cho DJ = $\frac{2}{3}$DO.

Mà OA và OD là hai tia đối nhau nên A, I, O, J, D thẳng hàng.

Do AI = $\frac{2}{3}$AO nên OI = $\frac{1}{3}$AO.

Do DJ = $\frac{2}{3}$DO nên OJ = $\frac{1}{3}$DO.

Do AO = DO và I, O, J thẳng hàng nên IJ = OI + OJ = $\frac{2}{3}$AO.

Khi đó AI = $\frac{2}{3}$AO, IJ = $\frac{2}{3}$AO, DJ = $\frac{2}{3}$AO nên AI = IJ = JD.

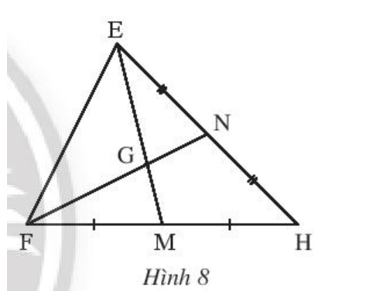
Bài 1 trang 75 Toán 7 Tập 2: Quan sát Hình 8. Thay $\overline{)?}$bằng số thích hợp.

EG = $\overline{)?}$EM;GM = $\overline{)?}$EM;GM = $\overline{)?}$EG;

FG = $\overline{)?}$GN;FN = $\overline{)?}$GN;FN = $\overline{)?}$FG.

Lời giải:

Ta thấy G là giao điểm hai đường trung tuyến của tam giác EFH nên G là trọng tâm của tam giác EFH.

Do đó EG = $\frac{2}{3}$EM.

Suy ra GM = EM - EG = EM - $\frac{2}{3}$EM = $\frac{1}{3}$EM.

Khi đó GM : EG = $\frac{1}{3}$EM : $\frac{2}{3}$EM = $\frac{1}{2}$.

FG = $\frac{2}{3}$FN, do đó GN = FN - FG = FN - $\frac{2}{3}$FN = $\frac{1}{3}$FN.

Khi đó FG : GN = $\frac{2}{3}$FN : $\frac{1}{3}$FN = 2.

GN = $\frac{1}{3}$FN nên FN = 3GN.

FG = $\frac{2}{3}$FN nên FN = $\frac{3}{2}$FG.

Ta điền như sau:

EG = $\frac{2}{3}$EM;GM = $\frac{1}{3}$EM;GM = $\frac{1}{2}$EG;

FG = 2GN;FN = 3GN;FN = $\frac{3}{2}$FG.

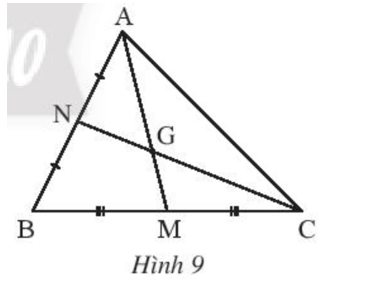
Bài 2 trang 75 Toán 7 Tập 2: Quan sát Hình 9.

a) Biết AM = 15 cm, tính AG.

b) Biết GN = 6 cm, tính CN.

Lời giải:

a) G là giao điểm hai đường trung tuyến của tam giác ABC nên G là trọng tâm của tam giác ABC.

Do đó AG = $\frac{2}{3}$AM = $\frac{2}{3}$. 15 = 10 cm.

b) Do G là trọng tâm của tam giác ABC nên GN = $\frac{1}{3}$>CN.

Do đó CN = 3GN = 3.6 = 18 cm.

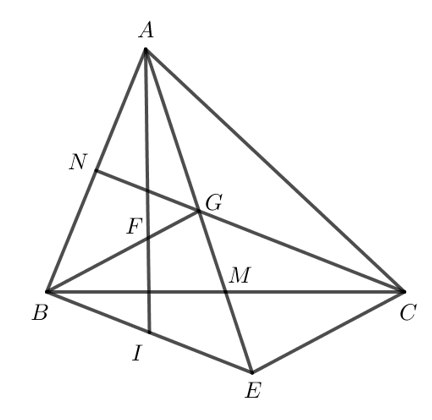
Bài 3 trang 75 Toán 7 Tập 2: Cho tam giác ABC. Hai đường trung tuyến AM và CN cắt nhau tại G. Trên tia đối của tia MA lấy điểm E sao cho ME = MG.

a) Chứng minh rằng BG song song với EC.

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC.

Lời giải:

a) Do AM là đường trung tuyến của tam giác ABC nên M là trung điểm của BC.

Do đó BM = CM.

Xét $△$BMG và $△$CME có:

BM = CM (chứng minh trên).

$\widehat{BMG}=\widehat{CME}$(đối đỉnh).

MG = ME (theo giả thiết).

Do đó $△$BMG = $△$CME (c.g.c).

Suy ra $\widehat{BGM}=\widehat{CEM}$(2 góc tương ứng).

Mà hai góc này ở vị trí so le trong nên BG // EC.

b) Do G là trọng tâm của tam giác ABC nên AG = 2GM.

Lại có ME = GM và G, M, E thẳng hàng nên GE = GM + ME = 2GM.

Suy ra AG = GE.

Do đó G là trung điểm của AE.

Tam giác ABE có hai đường trung tuyến AI và BG cắt nhau tại F nên F là trọng tâm của tam giác ABE.

Do đó AF = 2FI.

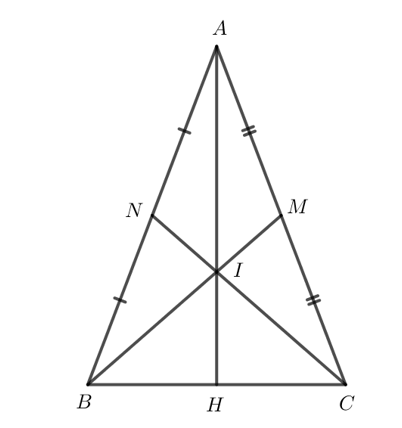
Bài 4 trang 75 Toán 7 Tập 2: Cho tam giác ABC cân tại A có BM và CN là hai đường trung tuyến.

a) Chứng minh rằng BM = CN.

b) Gọi I là giao điểm của BM và CN, đường thẳng AI cắt BC tại H. Chứng minh H là trung điểm của BC.

Lời giải:

a) Do tam giác ABC cân tại A nên AB = AC và $\widehat{ABC}=\widehat{ACB}$.

Do BM và CN là các đường trung tuyến của tam giác ABC nên M và N là lần lượt là trung điểm của AC và AB.

Khi đó BN = $\frac{1}{2}$AB, CM = $\frac{1}{2}$AC.

Mà AB = AC nên BN = CM.

Xét $\Delta MCB$và $\Delta NBC$có:

MC = NB (chứng minh trên).

$\widehat{MCB}=\widehat{NBC}$(chứng minh trên).

BC chung.

Do đó $\Delta MCB=\Delta NBC$(c.g.c).

Suy ra BM = NC (2 cạnh tương ứng).

b) Tam giác ABC có hai đường trung tuyến BM và CN cắt nhau tại I nên I là trọng tâm của tam giác ABC.

Khi đó AI đi qua trung điểm của BC.

Mà AI cắt BC tại H nên H là trung điểm của BC.

Lời giải bài tập Toán lớp 7 Bài 7: Tính chất ba đường trung tuyến của tam giác Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 73 Tập 2

• Giải Toán 7 trang 74 Tập 2

• Giải Toán 7 trang 76 Tập 2