Giải Toán 7 trang 76 Tập 2 Chân trời sáng tạo

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 76 Tập 2 trong Bài 7: Tính chất ba đường trung tuyến của tam giác Toán lớp 7 Tập 2 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 76.

Giải Toán 7 trang 76 Tập 2 Chân trời sáng tạo

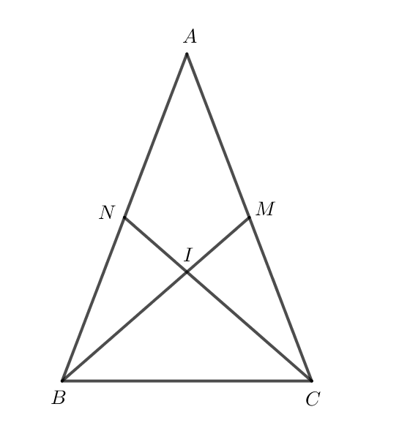
Bài 5 trang 76 Toán 7 Tập 2: Cho tam giác ABC có đường trung tuyến BM bằng trung tuyến CN. Chứng minh rằng tam giác ABC cân.

Lời giải:

Gọi giao điểm của BM và CN là I.

Tam giác ABC có I là giao điểm hai đường trung tuyến nên I là trọng tâm của tam giác ABC.

Khi đó BI = $\frac{2}{3}$BM, IM = $\frac{1}{3}$BM, CI = $\frac{2}{3}$CN, IN = $\frac{1}{3}$CN.

Mà BM = CN nên BI = CI, IM = IN.

Xét $\Delta NIB$và $\Delta MIC$có:

IN = IM (chứng minh trên).

$\widehat{NIB}=\widehat{MIC}$(đối đỉnh).

IB = IC (chứng minh trên).

Do đó $\Delta NIB=\Delta MIC$(c.g.c).

Suy ra BN = CM (2 cạnh tương ứng).

Do BM và CN là các đường trung tuyến của tam giác ABC nên M và N lần lượt là trung điểm của AC và AB.

Suy ra BN = $\frac{1}{2}$AB, CM = $\frac{1}{2}$AC.

Do đó AB = AC.

Tam giác ABC có AB = AC nên tam giác ABC cân tại A.

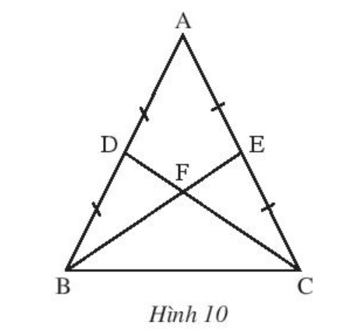
Bài 6 trang 76 Toán 7 Tập 2: Cho tam giác ABC cân tại A có BE và CD là hai đường trung tuyến cắt nhau tại F (Hình 10). Biết BE = 9 cm, tính độ dài đoạn thẳng DF.

Lời giải:

Tam giác ABC cân tại A nên AB = AC.

BE và CD là hai đường trung tuyến của tam giác ABC nên E và D lần lượt là trung điểm của AC, AB.

Suy ra AE = $\frac{1}{2}$AC, AD = $\frac{1}{2}$AB.

Mà AB = AC nên AE = AD.

Xét $\Delta ABE$và $\Delta AC\text{D}$có:

AB = AC (chứng minh trên).

$\hat{A}$chung.

AE = AD (chứng minh trên).

Do đó $\Delta ABE=\Delta AC\text{D}$(c.g.c).

Suy ra BE = CD (2 cạnh tương ứng).

F là giao điểm hai đường trung tuyến trong tam giác ABC nên F là trọng tâm của tam giác ABC.

Do đó DF = $\frac{1}{3}$CD = $\frac{1}{3}$. 9 = 3 (cm).

Vậy DF = 3 cm.

Lời giải bài tập Toán lớp 7 Bài 7: Tính chất ba đường trung tuyến của tam giác Chân trời sáng tạo hay khác:

• Giải Toán 7 trang 73 Tập 2

• Giải Toán 7 trang 74 Tập 2

• Giải Toán 7 trang 75 Tập 2