a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường
Câu hỏi:
a) Chứng minh rằng trong tam giác ABC cân tại A, đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác đó.
Trả lời:
a)
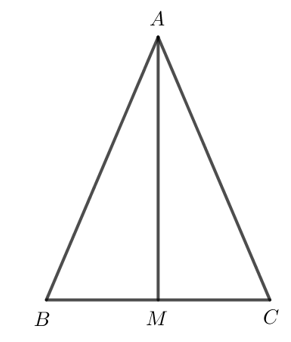
Gọi M là trung điểm của BC.
Khi đó M nằm trên đường trung trực của BC.
Do tam giác ABC cân tại A nên AB = AC
Do đó A nằm trên đường trung trực của BC.
Suy ra AM là đường trung trực của BC nên AM ⊥ BC.
Vì vậy AM là đường cao của tam giác ABC.
Xét DABM và DACM có:
AB = AC (do DABC cân tại A),
BM = CM (do M là trung điểm của BC),
AM là cạnh chung
Do đó DABM = DACM (c.c.c)
Suy ra 
(hai góc tương ứng)
Nên AM là tia phân giác của 
.
Vậy đường trung trực của cạnh BC là đường cao và cũng là đường phân giác xuất phát từ đỉnh A của tam giác ABC.
