Câu hỏi:
c) Tìm khoảng cách từ điểm C đến đường thẳng AB.
Trả lời:
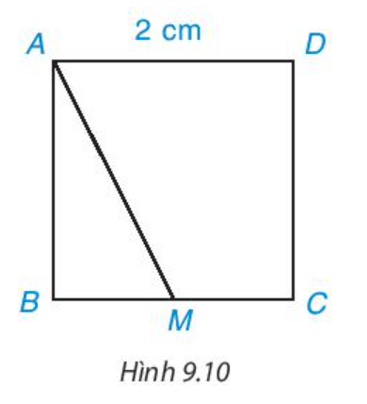
c) Đường vuông góc kẻ từ điểm C đến đường thẳng AB là CB.
Khoảng cách từ C đến đường thẳng AB bằng độ dài đoạn BC.
Do ABCD là hình vuông nên BC vuông góc với AB tại B. Do đó, BC = AD = 2 cm.
Vậy khoảng cách từ C đến đường thẳng AB bằng 2 cm.
Câu 1:
Bạn Nam tập bơi ở một bể bơi hình chữ nhật, trong đó có ba đường bơi OA, OB và OC. Biết rằng OA vuông góc với cạnh của bể bơi (H.9.8).
Nếu xuất phát từ điểm O và bơi cùng tốc độ, để bơi sang bờ bên kia nhanh nhất thì bạn Nam nên chọn đường bơi nào?
Câu 2:
Cho điểm A không nằm trên đường thẳng d.
a) Hãy vẽ đường vuông góc AH và một đường xiên AM từ A đến d.
Câu 4:
Cho hình vuông ABCD có độ dài cạnh bằng 2 cm, M là một điểm trên cạnh BC như Hình 9.10.
a) Hãy chỉ ra các đường vuông góc và đường xiên kẻ từ điểm A đến đường thẳng BC.
Câu 6:
a) Quan sát Hình 9.11, ta thấy khi M thay đổi trên d, M càng xa H thì độ dài AM càng lớn, tức là nếu HM < HN thì AM < AN. Hãy chứng minh khẳng định này nhờ quan hệ giữa góc và cạnh đối diện trong tam giác AMN.
Câu 7:
b) Xét hình vuông ABCD và một điểm M tùy ý nằm trên các cạnh của hình vuông. Hỏi với vị trí nào của M thì AM lớn nhất? Vì sao?
Câu 8:
Chiều cao của tam giác ứng với một cạnh của nó có phải là khoảng cách từ đỉnh đối diện đến đường thẳng chứa cạnh đó không?
