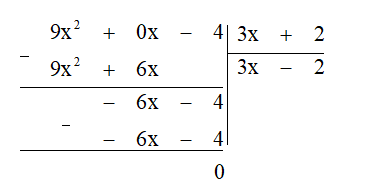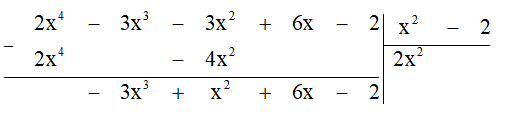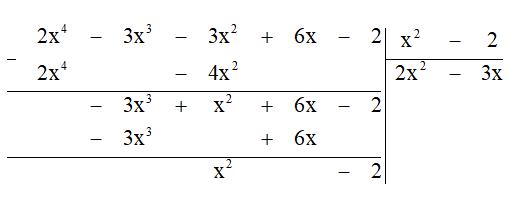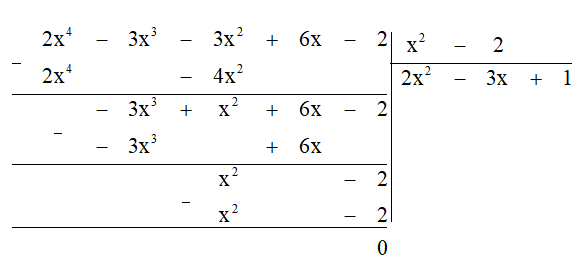Giải Toán 7 trang 41 Tập 2 Kết nối tri thức

---

Haylamdo biên soạn và sưu tầm với giải Toán 7 trang 41 Tập 2 trong Bài 28: Phép chia đa thức một biến Toán lớp 7 Tập 2 Kết nối tri thức hay nhất, chi tiết sẽ giúp học sinh dễ dàng trả lời các câu hỏi & làm bài tập Toán 7 trang 41.

Giải Toán 7 trang 41 Tập 2 Kết nối tri thức

Câu hỏi trang 41 Toán 7 Tập 2: Kiểm tra lại rằng ta có phép chia hết A : B = 2x² - 5x + 1, nghĩa là xảy ra

A = B . (2x² - 5x + 1).

Lời giải:

Ta có B . (2x² - 5x + 1) = (x² - 4x - 3) . (2x² - 5x + 1)

= x².(2x² - 5x + 1) + (-4x).(2x² - 5x + 1) + (-3).(2x² - 5x + 1)

= x² . 2x² + x² . (-5x) + x² . 1 + (-4x) . 2x² + (-4x) . (-5x) + (-4x) . 1 + (-3) . 2x²

+ (-3) . (-5x) + (-3) . 1

= 2x⁴ - 5x³ + x² - 8x³ + 20x² - 4x - 6x² + 15x - 3

= 2x⁴ + (-5x³ - 8x³) + (x² + 20x² - 6x²) + (-4x + 15x) - 3

= 2x⁴ - 13x³ + 15x² + 11x - 3

= A.

Vậy ta có phép chia hết A : B = 2x² - 5x + 1.

Luyện tập 2 trang 41 Toán 7 Tập 2: Thực hiện phép chia:

a) (-x⁶ + 5x⁴ - 2x³) : 0,5x².

b) (9x² - 4) : (3x + 2).

Lời giải:

a) (-x⁶ + 5x⁴ - 2x³) : 0,5x²

= -x⁶ : 0,5x² + 5x⁴ : 0,5x² + (-2x³) : 0,5x²

= (-1 : 0,5) . (x⁶ : x²) + (5 : 0,5) . (x⁴ : x²) + (-2 : 0,5) . (x³ : x²)

= (-1 : )x⁴ + (5 : )x² + (-2 : )x

= (-1 . 2)x⁴ + (5 . 2)x² + (-2 . 2)x

= -2x⁴ + 10x² - 4x

b) Thực hiện theo các bước sau:

Bước 1. Lấy hạng tử có bậc cao nhất của đa thức 9x² - 4 chia cho hạng tử có bậc cao nhất của đa thức 3x + 2:

9x² : 3x = 3x.

Bước 2. Lấy đa thức 9x² - 4 trừ đi (3x + 2).3x ta được dư thứ nhất là -6x - 4.

Bước 3. Lấy hạng tử có bậc cao nhất của dư thứ nhất chia cho hạng tử có bậc cao nhất của đa thức 3x + 2:

-6x : 3x = -2.

Bước 4. Lấy dư thứ nhất trừ đi -2(3x + 2) ta được dư thứ hai là 0 nên quá trình chia kết thúc.

Vậy (9x² - 4) : (3x + 2) = 3x - 2.

Vận dụng trang 41 Toán 7 Tập 2: Em hãy giải bài toán trong tình huống mở đầu

Lời giải:

Thực hiện theo các bước sau:

Bước 1. Lấy hạng tử có bậc cao nhất của A chia cho hạng tử có bậc cao nhất của B:

2x⁴ : x² = 2x².

Bước 2. Lấy A trừ đi tích B. 2x² ta được dư thứ nhất là -3x³ + x² + 6x - 2.

Bước 3. Lấy hạng tử cao nhất của dư thứ nhất chia cho hạng tử bậc cao nhất của B:

(-3x³) : x² = -3x.

Bước 4. Lấy dư thứ nhất trừ đi tích B. (-3x) ta được dư thứ hai là x² - 2.

Bước 5. Lấy hạng tử cao nhất của dư thứ hai chia cho hạng tử bậc cao nhất của B:

x² : x² = 1.

Bước 6. Lấy dư thứ nhất trừ đi tích B. 1 ta được dư thứ ba là 0.

Bước 7. Dư cuối cùng bằng 0 nên quá trình chia kết thúc.

Vậy A : B = 2x² - 3x + 1.

Lời giải bài tập Toán lớp 7 Bài 28: Phép chia đa thức một biến Kết nối tri thức hay khác:

• Giải Toán 7 trang 39 Tập 2

• Giải Toán 7 trang 40 Tập 2

• Giải Toán 7 trang 42 Tập 2

• Giải Toán 7 trang 43 Tập 2