Bài 4 trang 65 Toán 8 Tập 2 Cánh diều
Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.
Giải Toán 8 Bài 3: Đường trung bình của tam giác - Cánh diều
Bài 4 trang 65 Toán 8 Tập 2: Cho tam giác ABC nhọn có H là trực tâm. Gọi M, N, P, Q lần lượt là trung điểm của các đoạn thẳng AB, BH, HC, CA. Chứng minh tứ giác MNPQ là hình chữ nhật.
Lời giải:
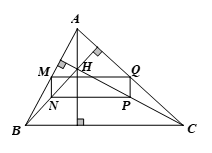
⦁Xét ∆ABH có M, N lần lượt là trung điểm của AB, BH nên MN là đường trung bình ∆ABH.
Suy ra MN//AH (1)
Tương tự, xét ∆AHC ta cũng có PQ là đường trung bình ∆AHC nên PQ//AH (2)
Từ (1) và (2) ta có MN // PQ // AH.
⦁ Chứng minh tương tự như trên với ∆ABC và ∆HBC, ta cũng có MQ, NP lần lượt là đường trung bình của ∆ABC và ∆HBC.
Do đó MQ // BC và NP // BC. Suy ra MQ // NP // BC.
Tứ giác MNPQ có MN // PQ và MQ // NP nên MNPQ là hình bình hành.
⦁ Ta có MN//AH và AH ⊥ BC (do H là trực tâm của ∆ABC) nên MN ⊥ BC
Lại có NP // BC nên suy ra MN ⊥ NP hay
Hình bình hành MNPQ có nên MNPQ là hình chữ nhật.
Lời giải bài tập Toán 8 Bài 3: Đường trung bình của tam giác hay, chi tiết khác:
Luyện tập 1 trang 62 Toán 8 Tập 2: Vẽ tam giác ABC và các đường trung bình của tam giác đó ....
Hoạt động 2 trang 63 Toán 8 Tập 2: Cho tam giác ABC có MN là đường trung bình (Hình 31) ....
