Bài 4 trang 94 Toán 8 Tập 2 Cánh diều

Cho tứ giác ABCD. Tia phân giác của góc BAD và BCD cắt nhau tại điểm I . Chứng minh AB.CD = AD.BC.

Giải Toán 8 Bài tập cuối chương 8 - Cánh diều

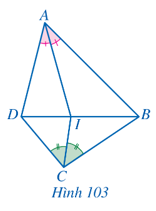
Bài 4 trang 94 Toán 8 Tập 2: Cho tứ giác ABCD. Tia phân giác của góc BAD và BCD cắt nhau tại điểm I (Hình 103). Chứng minh AB.CD = AD.BC.

Lời giải:

Xét ∆ABD có AI là phân giác của góc BAD nên $\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{AB}}{\mathrm{AD}}$  (tính chất đường phân giác)

Xét ∆BCD có CI là phân giác của góc BCD nên $\frac{\mathrm{IB}}{\mathrm{ID}}=\frac{\mathrm{CB}}{\mathrm{CD}}$  (tính chất đường phân giác)

Suy ra $\frac{\mathrm{AB}}{\mathrm{AD}}=\frac{\mathrm{CB}}{\mathrm{CD}},$  do đó AB.CD = AD.BC.

Lời giải bài tập Toán 8 Bài tập cuối chương 8 hay, chi tiết khác:

• Bài 1 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, $\hat{E}=60°,$ $\hat{M}=40°.$ a) Số đo góc D bằng bao nhiêu độ? ....

• Bài 2 trang 94 Toán 8 Tập 2: Cho ∆DEG ᔕ ∆MNP, DE = 2 cm, DG = 4 cm, MN = 4 cm, NP = 6 cm. a) Độ dài cạnh EG là ....

• Bài 3 trang 94 Toán 8 Tập 2: Cho tam giác ABC, các điểm M, N, P lần lượt thuộc các cạnh AB, AC, BC sao cho ....

• Bài 5 trang 94 Toán 8 Tập 2: Cho hình bình hành ABCD. Gọi M, N, P lần lượt là trung điểm các đoạn thẳng AB ....

• Bài 6 trang 95 Toán 8 Tập 2: Cho ∆ABC ᔕ ∆A’B’C’ với tỉ số đồng dạng k. a) Gọi AM, AM’ lần lượt là các đường trung tuyến ....

• Bài 7 trang 95 Toán 8 Tập 2: Tính các độ dài x, y, z, t ở các hình 104a, 104b, 104c: ....

• Bài 8 trang 95 Toán 8 Tập 2: Cho Hình 105. Chứng minh: a) ∆HAB ᔕ ∆HBC; b) HB = HD = 6 cm ....

• Bài 9 trang 95 Toán 8 Tập 2: Cho Hình 106. Chứng minh: a) AH² = AB.AI = AC.AK; b) $\widehat{\mathrm{AIK}}=\widehat{\mathrm{ACH}}.$  ....

• Bài 10 trang 96 Toán 8 Tập 2: Cho tam giác ABC có M, N là hai điểm lần lượt thuộc các cạnh AB, AC sao cho MN // BC ....

• Bài 11 trang 96 Toán 8 Tập 2: Cho Hình 107. Chứng minh: a) ∆ABN ᔕ ∆AIP và AI.AN = AP.AB ....

• Bài 12 trang 96 Toán 8 Tập 2: Hình 108 minh họa mặt cắt đứng của tủ sách nghệ thuật ở nhà bác Ngọc. Sau một thời gian sử dụng ....

• Bài 13 trang 96 Toán 8 Tập 2: Cho Hình 109. Hình nào đồng dạng phối cảnh với: a) Tam giác OAB? ....

• Bài 14 trang 96 Toán 8 Tập 2: Hình 110 có ghi thứ tự của 6 lá mầm, trong đó có nhiều cặp lá mầm gợi nên những cặp hình đồng dạng ....