Hoạt động 2 trang 113, 114 Toán 8 Tập 1 Cánh diều

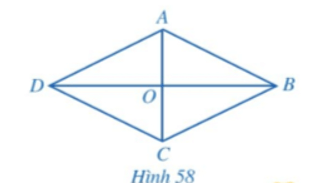
Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (Hình 58).

Giải Toán 8 Bài 6: Hình thoi - Cánh diều

Hoạt động 2 trang 113, 114 Toán 8 Tập 1: Cho hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (Hình 58).

Hoạt động 2 trang 113, 114 Toán 8 Tập 1 Cánh diều | Giải Toán 8

a) Hình thoi ABCD có là hình bình hành hay không?

b) Hai đường chéo AC và BD có vuông góc với nhau hay không?

c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của $\hat{B A D}$ hay không?

Lời giải:

a) Do ABCD là hình thoi nên AB = BC = CD = DA.

Xét tứ giác ABCD có: AB = CD, AD = BC nên ABCD là hình bình hành.

b) Do ABCD là hình bình hành nên OB = OD.

Xét ΔOAD và ΔOAB có:

OA là cạnh chung;

AD = AB (chứng minh trên);

OD = OB (chứng minh trên).

Do đó ΔOAD = ΔOAB (c.c.c)

Suy ra $\hat{A O D} = \hat{A O B}$ (hai góc tương ứng)

Mà $\hat{A O D} + \hat{A O B} = 180 °$ _. (hai góc kề bù)

Do đó $\hat{A O D} = \hat{A O B} = \frac{180 °}{2} = 90 °$ hay AC ⊥ BD tại O.

c) Xét ΔABC và ΔADC có:

AC là cạnh chung;

AB = AD (chứng minh câu a);

BC = DC (chứng minh câu a)

Do đó ΔABC = ΔADC (c.c.c)

Suy ra $\hat{B A C} = \hat{D A C}$ (hai góc tương ứng)

Nên AC là tia phân giác của $\hat{B A D}$ .

Lời giải bài tập Toán 8 Bài 6: Hình thoi hay, chi tiết khác: