Bài 4.24 trang 89 Toán 8 Tập 1 | Kết nối tri thức Giải Toán 8
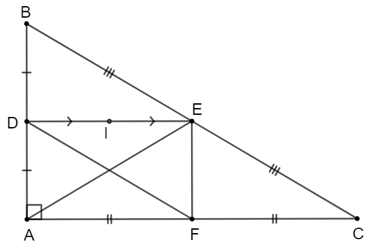
Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
Giải Toán 8 Bài tập cuối chương 4 - Kết nối tri thức
Bài 4.24 trang 89 Toán 8 Tập 1: Cho tam giác ABC vuông tại A. Gọi D, E, F lần lượt là trung điểm của AB, BC, AC.
a) Chứng minh rằng AE = DF.
b) Gọi I là trung điểm của DE. Chứng minh rằng ba điểm B, I, F thẳng hàng.
Lời giải:
a) Theo đề bài, tam giác ABC vuông tại A nên hay AB ⊥ AC.
Vì D, E lần lượt là trung điểm của AB, BC nên DE là đường trung bình của tam giác ABC suy ra DE // AC.
Mà AB ⊥ AC nên AB ⊥ DE hay .
Tương tự, ta chứng minh được: EF ⊥ AC hay .
Ta có:
Suy ra .
Tứ giác ADEF có .
Do đó tứ giác ADEF là hình chữ nhật.
Suy ra hai đường chéo AE và DF bằng nhau.
Vậy AE = DF (đpcm).
b) Vì D, F lần lượt là trung điểm của AB, AC nên DF là đường trung bình của tam giác ABC.
Suy ra DF // BC hay DF // BE.
Vì tứ giác ADEF là hình chữ nhật nên AD // EF hay BD // EF.
Tứ giác BDFE có DF // BE và BD // EF nên tứ giác BDFE là hình bình hành.
Hình bình hành BDFE có hai đường chéo BF và DE.
Mà I là trung điểm của DE nên I cũng là trung điểm của BF.
Do đó, ba điểm B, I, F thẳng hàng.
Lời giải bài tập Toán 8 Bài tập cuối chương 4 hay, chi tiết khác:
Bài 4.18 trang 89 Toán 8 Tập 1: Độ dài x trong Hình 4.31 bằng ....
Bài 4.19 trang 89 Toán 8 Tập 1: Cho tam giác ABC. Gọi H, K lần lượt là trung điểm của AC, BC ....