Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong
Câu hỏi:
Cắt bốn tứ giác như nhau bằng giấy rồi đánh số bốn góc của mỗi tứ giác như tứ giác ABCD trong Hình 3.1a. Ghép bốn tứ giác giấy đó để được hình như Hình 3.1b.
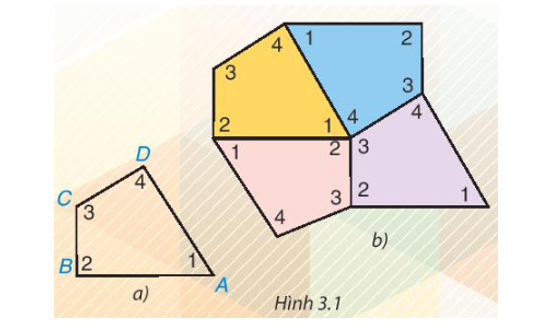
- Em có thể ghép bốn tứ giác khít nhau như vậy không?
- Em có nhận xét gì về bốn góc tại điểm chung của bốn tứ giác? Hãy cho biết tổng số đoTrả lời:
- Em cắt bốn tứ giác như nhau bằng giấy rồi thực hiện các bước theo yêu cầu bài toán.
Ta có thể ghép bốn tứ giác khít nhau như Hình 3.1b.
- Nhận xét: Bốn góc tại điểm chung của bốn tứ giác được ghép khít nhau.
Khi đó: