Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu
Câu hỏi:
Cho hai tam giác đồng dạng. Tam giác thứ nhất có độ dài ba cạnh là 4 cm, 8 cm và 10 cm. Tam giác thứ hai có chu vi là 33 cm. Độ dài ba cạnh của tam giác thứ hai là bộ ba nào sau đây?
a) 6 cm, 12 cm, 15 cm. b) 8 cm, 16 cm, 20 cm.
c) 6 cm, 9 cm, 18 cm. d) 8 cm, 10 cm, 15 cm.
Trả lời:
Vì 6 + 12 + 15 = 33 (cm) và nên bộ ba trong câu a) là độ dài ba cạnh của tam giác thỏa mãn yêu cầu. Các bộ ba còn lại hoặc không có tổng bằng 33 cm hoặc không có tỉ lệ tương ứng với (4 : 8 : 10) nên không thể là độ dài ba cạnh của tam giác thỏa mãn yêu cầu.
Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:
Câu 1:
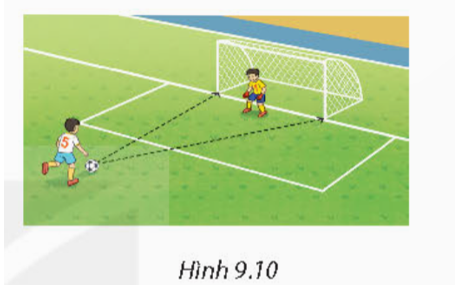
Trong môn Bóng đá, độ khó của mỗi pha ghi bàn còn được tính bởi góc sút vào cầu môn là rộng hay hẹp. Nếu biết độ rộng của khung thành là 7,32 m, trái bóng cách hai cột gôn lần lượt là 10,98 m và 14,64 m thì em có cách nào để đo được góc sút ở vị trí này bởi các dụng cụ học tập không?
Xem lời giải »
Câu 2:
Cho hai tam giác ABC và A'B'C' có .
a) Nếu A′B' = AB thì hai tam giác có đồng dạng với nhau không? Vì sao?
Xem lời giải »
Câu 3:
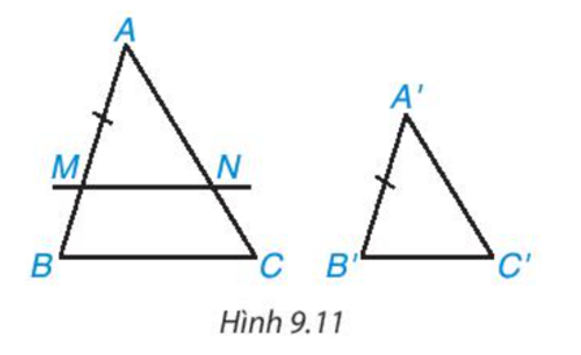
b) Nếu A′B' < AB như Hình 9.11. Trên đoạn thẳng AB lấy điểm M sao cho AM = A′B′. Kẻ đường thẳng qua M song song với BC và cắt AC tại N.
- Hãy giải thích vì sao ΔAMN ∽ ΔABC.
- Hãy chứng tỏ rằng AN = A′C′, MN = B′C′ để suy ra ΔAMN = ΔA'B'C' (c.c.c).
- Hai tam giác A'B'C' và ABC có đồng dạng với nhau không? Nếu có, em hãy viết đúng kí hiệu đồng dạng giữa chúng.
Xem lời giải »
Câu 4:
c) Nếu A'B' > AB thì tam giác A'B'C' có đồng dạng với tam giác ABC không? Vì sao?
Xem lời giải »
Câu 5:
Cho AM, BN, CP là các đường trung tuyến của tam giác ABC. Cho A'M', B'N', C'P' là các đường trung tuyến của tam giác A'B'C'. Biết rằng ΔA′B′C′ ∽ ΔABC.
Chứng minh rằng .
Xem lời giải »
Câu 6:
Cho tam giác ABC có AB = 12 cm, AC = 15 cm. Trên các tia AB, AC lần lượt lấy các điểm M, N sao cho AM = 10 cm, AN = 8 cm. Chứng minh rằng ΔABC ∽ ΔANM.
Xem lời giải »
Câu 7:
Cho góc BAC và các điểm M, N lần lượt trên các đoạn thẳng AB, AC sao cho .
a) Chứng minh rằng ΔABN ∽ ΔACM.
Xem lời giải »
Câu 8:
b) Gọi I là giao điểm của BN và CM. Chứng minh rằng IB . IN = IC . IM.
Xem lời giải »