Cho hàm số bậc nhất y = (m + 2)x + 3. a) Tìm m để đồ thị hàm số song song với đường thẳng y = –x.

Cho hàm số bậc nhất y = (m + 2)x + 3.

a) Tìm m để đồ thị hàm số song song với đường thẳng y = –x.

b) Vẽ đồ thị hàm số với giá trị m tìm được ở câu a.

c) Tìm giao điểm A của đồ thị hàm số tìm được ở câu a và đồ thị của hàm số y = x + 1. Tính diện tích của tam giác OAB, trong đó B là giao điểm của đồ thị hàm số y = x + 1 với trục Ox.

Hàm số y = (m + 2)x + 3 là hàm số bậc nhất khi m + 2 ≠ 0, hay m ≠ – 2.

Vậy ta có điều kiện m ≠ – 2.

a) Đồ thị hàm số đã cho song song với đường thẳng y = –x khi m + 2 = –1, tức là m = –3.

Giá trị này thỏa mãn điều kiện m ≠ – 2.

Vậy giá trị m cần tìm là m = –3.

b) Với m = –3 ta có hàm số y = –x + 3.

Đồ thị hàm số y = –x + 3 là đường thẳng đi qua hai điểm (0; 3) và (3; 0).

c) Phương trình hoành độ giao điểm của hai đồ thị hàm số y = –x + 3 và y = x + 1 là

– x + 3 = x + 1.

Giải phương trình trên ta được x = 1.

Từ đó suy ra y = 1 + 1 = 2.

Vậy giao điểm của hai đồ thị hàm số cần tìm là A(1; 2).

Giao điểm của đồ thị hàm số y = x + 1 với trục hoành Ox là B(–1; 0). Do đó OB = 1.

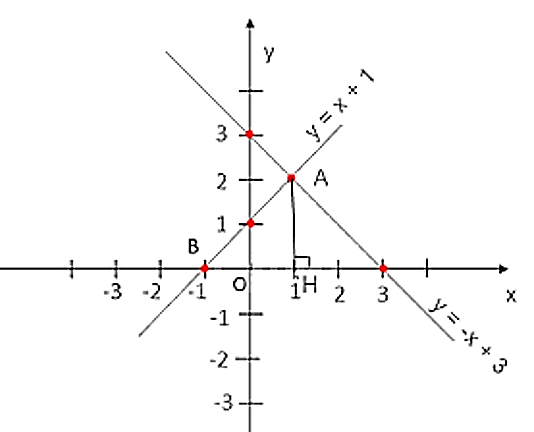
Gọi H là chân đường vuông góc hạ từ A xuống trục hoành. Khi đó AH là đường cao của tam giác OAB.

Ta thấy H(1; 0) và AH = |y_A| = 2.

Diện tích tam giác OAB là S_OAB = $\frac{1}{2}$AH . OB = $\frac{1}{2}$. 2 . 1 = 1 (đơn vị diện tích).