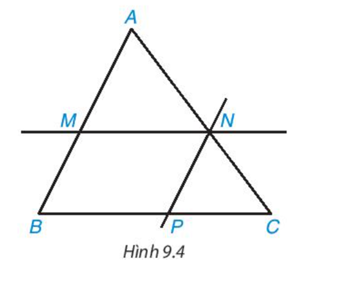
Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC như Hình 9.4.

Câu hỏi:

- Hãy viết các cặp góc bằng nhau của hai tam giác ABC và AMN, giải thích vì sao chúng bằng nhau.

- Kẻ đường thẳng đi qua N song song với AB và cắt BC tại P. Hãy chứng tỏ MN = BP và suy ra $\frac{M N}{B C} = \frac{A N}{A C} = \frac{A M}{A B}$ .

- Tam giác ABC và tam giác AMN có đồng dạng không? Nếu có hãy viết đúng kí hiệu đồng dạng.

Cho tam giác ABC và các điểm M, N lần lượt nằm trên các cạnh AB, AC sao cho MN song song với BC như Hình 9.4. (ảnh 1)

Trả lời:

- Các cặp góc bằng nhau của hai tam giác ABC và AMN:

$\hat{B} = \hat{A M N}; \hat{C} = \hat{A N M}$ (do MN // BC và các cặp góc này ở vị trí đồng vị);

$\hat{A}$ chung.

- Có MN // BP (vì MN // BC), MB // NP (vì AB // NP) nên MNPB là hình bình hành.

Suy ra MN = BP. Suy ra $\frac{M N}{B C} = \frac{B P}{B C} = \frac{A N}{A C} = \frac{A M}{A B}$ (Sử dụng định lí Thalès).

- Có $\hat{B} = \hat{A M N}; \hat{C} = \hat{A N M}$ ; $\hat{A}$ chung và $\frac{A M}{A B} = \frac{A N}{A C} = \frac{M N}{B C}$ , suy ra ∆ABC ∽ ∆AMN.

Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:

Câu 1:

Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn, bác Dương cắm một chiếc cọc gỗ (đoạn CD) thẳng đứng trên mặt đất rồi đo chiều dài bóng của cọc gỗ do ánh đèn điện tạo ra và đo khoảng cách từ điểm E đến chân cột đèn (điểm B) (H.9.1). Theo em bác Dương đã tính như thế nào để ra được chiều cao cột đèn?

Có một chiếc bóng điện được mắc trên đỉnh (Điểm A) của cột đèn thẳng đứng. Để tính chiều cao AB của cột đèn (ảnh 1)

Xem lời giải »

Câu 2:

Trong hình 9.2, ΔABC và ΔDEF là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau, tức là AB // DE, AC // DF, BC // EF và $\hat{A} = \hat{D}, \hat{B} = \hat{E}, \hat{C} = \hat{F}$ . Nhìn hình vẽ, hãy cho biết giá trị của các tỉ số sau: $\frac{A B}{D E}; \frac{B C}{E F}; \frac{A C}{D F}$ .

Trong hình 9.2, ΔABC và ΔDEF là hai tam giác có các cạnh tương ứng song song và các góc tương ứng bằng nhau (ảnh 1)

Xem lời giải »

Câu 3:

Trong các tam giác được vẽ trên ô lưới vuông (H.9.3), có một cặp tam giác đồng dạng. Hãy chỉ ra cặp tam giác đó, viết đúng kí hiệu đồng dạng và tìm tỉ số đồng dạng của chúng.