Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.
Câu hỏi:
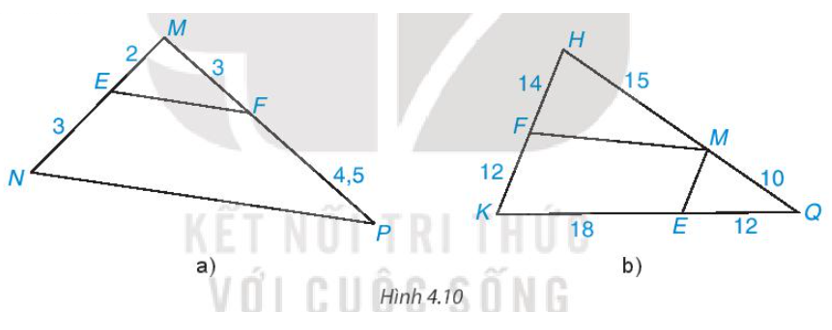
Tìm các cặp đường thẳng song song trong Hình 4.10 và giải thích tại sao chúng song song với nhau.
Trả lời:
• Hình 4.10a)
Ta có nên .
Vì , E ∈ MN, F ∈ MP nên theo định lí Thalès đảo ta suy ra EF // MN.
• Hình 4.10b)
* Ta có: .
Vì nên MF không song song với KQ.
* Ta có: .
Vì ; F ∈ HK; M ∈ HQ nên theo định lí Thalès đảo ta suy ra ME // HK.
Xem thêm lời giải bài tập Toán 8 Kết nối tri thức hay, chi tiết:
Câu 1:
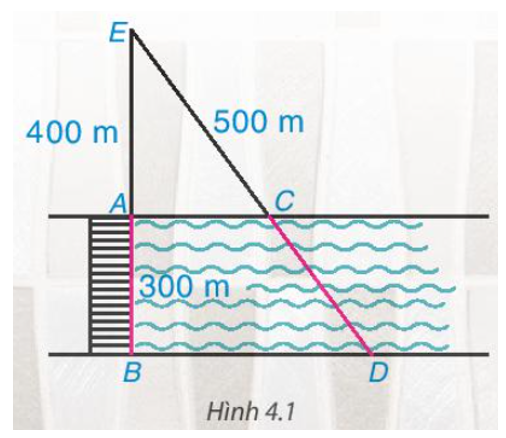
Cây cầu AB bắc qua một con sông có chiều rộng 300 m. Để đo khoảng cách giữa hai điểm C và D trên hai bờ con sông, người ta chọn một điểm E trên đường thẳng AB sao cho ba điểm E, C, D thẳng hàng. Trên mặt đất, người ta đo được AE = 400 m, EC = 500 m. Theo em, người ta tính khoảng cách giữa C và D như thế nào?
Xem lời giải »
Câu 2:
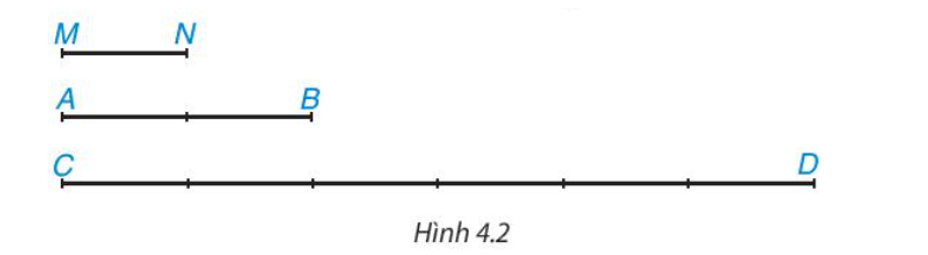
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
Hãy tìm độ dài của hai đoạn thẳng AB và CD nếu chọn đoạn MN làm đơn vị độ dài. Với các độ dài đó hãy tính tỉ số
Xem lời giải »
Câu 3:
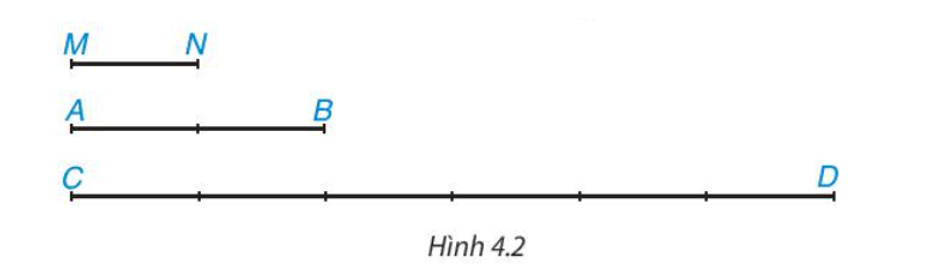
Cho Hình 4.2, em hãy thực hiện các hoạt động sau:
Dùng thước thẳng, đo độ dài hai đoạn thẳng AB và CD (đơn vị: cm) rồi dùng kết quả vừa đo để tính tỉ số .
Xem lời giải »
Câu 4:
So sánh hai tỉ số tìm được trong hai hoạt động trên.
Xem lời giải »
Câu 5:
Cho ∆ABC, từ điểm D trên cạnh BC, kẻ đường thẳng song song với AB cắt AC tại F và kẻ đường thẳng song song với AC cắt AB tại E.
Chứng minh rằng: .
Xem lời giải »
Câu 6:
Cho ∆ABC có trọng tâm G. Vẽ đường thẳng d qua G và song song với AB, d cắt BC tại điểm M. Chứng minh rằng .
Xem lời giải »
Câu 7:
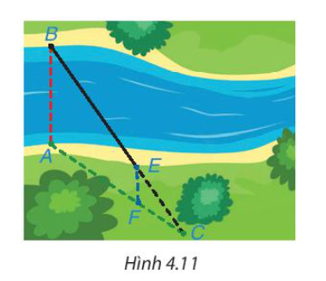
Để đo khoảng cách giữa hai vị trí B và E ở hai bên bờ sông, bác An chọn ba vị trí A, F, C cùng nằm ở một bên bờ sông sao cho ba điểm C, E, B thẳng hàng, ba điểm C, F, A thẳng hàng và AB // EF (H.4.11). Sau đó bác An đo được AF = 40 m, FC = 20 m, EC = 30 m. Hỏi khoảng cách giữa hai vị trí B và E bằng bao nhiêu?
Xem lời giải »