Trở lại tình huống mở đầu, ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC
Câu hỏi:
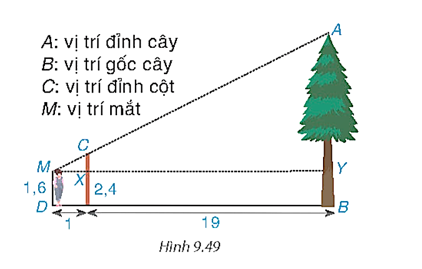
Trở lại tình huống mở đầu, ta thấy chiếc cột cùng với bóng của nó tạo thành hai cạnh góc vuông của tam giác ABC vuông tại đỉnh A, bạn Việt và bóng của mình cũng được xem là hai cạnh góc vuông của tam giác A'B'C' vuông tại đỉnh A' (H.9.48). Vì các tia sáng Mặt Trời tạo với hai cái bóng các góc bằng nhau nên .
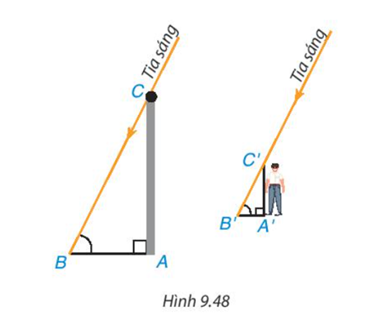
a) Hai tam giác vuông ABC và A'B'C' có đồng dạng với nhau không?
Trả lời:
a) Hai tam giác ABC vuông tại A và tam giác A'B'C' vuông tại A' có (giả thiết) nên ∆ABC ∽ ∆A'B'C'.