Trong Hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong
Câu hỏi:
Trong Hình 9.9, ABC là tam giác không cân; M, N, P lần lượt là trung điểm của BC, CA, AB. Hãy tìm trong hình năm tam giác khác nhau mà chúng đôi một đồng dạng với nhau. Giải thích vì sao chúng đồng dạng.
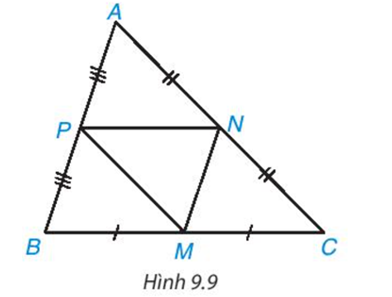
Trả lời:
- Do N, P lần lượt là trung điểm của CA, AB.
Suy ra PN là đường trung bình của tam giác ABC nên NP // BC (P ∈ AB, N ∈ AC).
Suy ra ΔABC ∽ ΔAPN.
- Do M, P lần lượt là trung điểm của BC, AB.
Suy ra MP là đường trung bình của tam giác ABC nên MP // AC (P ∈ AB, M ∈ BC)
Suy ra ΔABC ∽ ΔPBM.
- Do M, N lần lượt là trung điểm của BC, AC.
Suy ra MN là đường trung bình của tam giác ABC nên MN // AB (N ∈ AC, M ∈ BC).
Suy ra ΔABC ∽ ΔNMC.
- Ta có (do ΔABC ∽ ΔPBM); (do PN // BC); (do cùng bằng góc C); .
Do đó, ΔAPN ∽ ΔPBM.
- Tương tự ta cũng có ΔNMC ∽ ΔPBM.
- - Ta có ΔAPN = ΔMNP (g – c – g) vì ; (NP // BC và các cặp góc ở vị trí so le trong) và PN cạnh chung. Do đó ΔAPN ∽ ΔMNP.
Vậy ta có 5 tam giác APN, PBM, NMC, MNP, ABC đôi một đồng dạng với nhau.