Bài 2 trang 92 Toán 9 Tập 1 Cánh diều

Giải Toán 9 Bài tập cuối chương 4 - Cánh diều

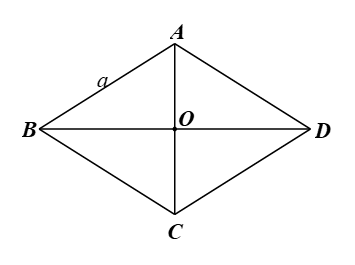
Bài 2 trang 92 Toán 9 Tập 1: Cho hình thoi ABCD có AB = a, $\widehat{BAD}=2\alpha \left(0°<\alpha <90°\right).$ Chứng minh:

a) BD = 2a.sinα;

b) AC = 2a.cosα.

Lời giải:

a) Gọi O là giao điểm của đường chéo AC và BD.

Vì ABCD là hình thoi nên AC ⊥ BD tại trung điểm O của mỗi đường và AC là đường phân giác của $\widehat{BAD}.$

Suy ra AC = 2AO, BD = 2BO và $\widehat{BAO}=\frac{1}{2}\widehat{BA\text{D}}=\frac{1}{2}\cdot 2\alpha =\alpha .$

Xét ∆ABO vuông tại O, ta có: BO = AB.sin$\widehat{BAO}$ = a.sin$\alpha$.

Do đó BD = 2BO = 2a.sinα.

b) Xét ∆ABO vuông tại O, ta có: AO = AB.cos$\widehat{BAO}$ = a.cos$\alpha$.

Do đó AC = 2AO = 2a.cosα.

Lời giải bài tập Toán 9 Bài tập cuối chương 4 hay, chi tiết khác:

• Bài 1 trang 92 Toán 9 Tập 1: Cho tam giác ABC vuông tại A có đường cao AH và $\hat{B}=\alpha$ (Hình 40) ....

• Bài 3 trang 92 Toán 9 Tập 1: Trong trò chơi xích đu ở Hình 41, khi dây căng xích đu (không dãn) OA = 3 m ....

• Bài 4 trang 92 Toán 9 Tập 1: Một người đứng ở vị trí B trên bờ sông muốn sử dụng la bàn ....