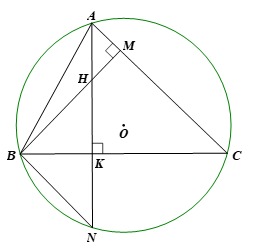
Bài 3 trang 79 Toán 9 Tập 2 Cánh diều
Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AK, BM cắt nhau tại trực tâm H của tam giác ABC. Tia AK cắt đường tròn (O) tại điểm N (khác A). Chứng minh:
Giải Toán 9 Bài tập cuối chương 8 - Cánh diều
Bài 3 trang 79 Toán 9 Tập 2: Cho tam giác nhọn ABC nội tiếp đường tròn (O). Các đường cao AK, BM cắt nhau tại trực tâm H của tam giác ABC. Tia AK cắt đường tròn (O) tại điểm N (khác A). Chứng minh:
a)
b) Tam giác BHN cân;
c) BC là đường trung trực của HN.
Lời giải:
a) Xét ∆ABC có các đường cao AK, BM cắt nhau tại trực tâm H nên AK ⊥ BC và BM ⊥ AC.
Vì ∆AKC vuông tại K có (tổng hai góc nhọn của tam giác vuông bằng 90°).
Vì ∆BMC vuông tại M có (tổng hai góc nhọn của tam giác vuông bằng 90°).
Suy ra
b) Xét đường tròn (O) có là hai góc nội tiếp cùng chắn cung CN nên hay
Mà (câu a) nên hay
Do đó BK là đường phân giác của góc HBN.
Xét ∆BHN có đường cao BK đồng thời là đường phân giác nên ∆BHN cân tại B.
c) Vì ∆BHN cân tại B (câu b) nên đường cao BK đồng thời là đường trung trực của HN.
Vậy BC đường trung trực của HN.
Lời giải bài tập Toán 9 Bài tập cuối chương 8 hay, chi tiết khác: