Bài 4 trang 79 Toán 9 Tập 2 Cánh diều

Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh:

Giải Toán 9 Bài tập cuối chương 8 - Cánh diều

Bài 4 trang 79 Toán 9 Tập 2: Cho tứ giác nội tiếp ABCD có hai tia CD và BA cắt nhau tại I. Chứng minh:

a) $\hat{I A D} = \hat{B C D};$

b) IA . IB = ID . IC.

Lời giải:

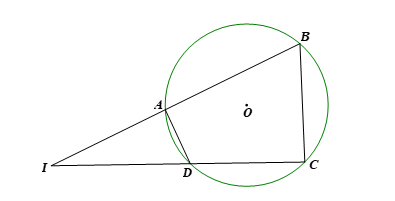
Bài 4 trang 79 Toán 9 Tập 2 Cánh diều | Giải Toán 9

a) Vì tứ giác ABDC nội tiếp đường tròn (O) nên các góc đối diện có tổng số đo bằng 180°. Do đó: $\hat{B A D} + \hat{B C D} = 180 °$

Mà $\hat{B A D} + \hat{I A D} = 180 °$ (hai góc kề bù) nên $\hat{I A D} = \hat{B C D} .$

b) Xét ∆IAD và ∆ICB, có:

$\hat{I A D} = \hat{I C D}$ (do $\hat{I A D} = \hat{B C D})$ và $\hat{B I C}$ là góc chung

Do đó ∆IAD ᔕ ∆ICB (g.g)

Suy ra $\frac{I A}{I C} = \frac{I D}{I B}$ (tỉ số đồng dạng) nên IA . IB = IC . ID.

Lời giải bài tập Toán 9 Bài tập cuối chương 8 hay, chi tiết khác: