c) Hai dây bằng nhau thì cách đều tâm;
Câu hỏi:
c) Hai dây bằng nhau thì cách đều tâm;
Trả lời:
c)
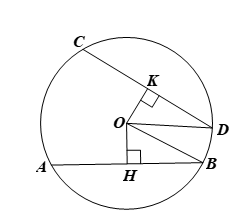
Gọi (O) là đường tròn có hai dây AB, CD. Gọi OH, OK lần lượt là khoảng cách từ O đến AB, CD. Khi đó OH ⊥ AB tại H và OK ⊥ CD tại K.
Do đó, theo kết quả của câu a, ta có: H, K lần lượt là trung điểm của AB, CD.
Suy ra và
Mà AB = CD nên HB = KD. (1)
Xét ∆OHB vuông tại H, ta có: OB2 = OH2 + HB2 (định lí Pythagore).
Suy ra OH2 = OB2 – HB2 = R2 – HB2. (2)
Xét ∆OKD vuông tại H, ta có: OD2 = OK2 + KD2 (định lí Pythagore).
Suy ra OK2 = OD2 – KD2 = R2 – KD2. (3)
Từ (1), (2) và (3) suy ra OH2 = OK2, hay OH = OK.
Vậy hai dây bằng nhau thì cách đều tâm.
Xem thêm lời giải bài tập Toán 9 Cánh diều hay, chi tiết:
Câu 1:
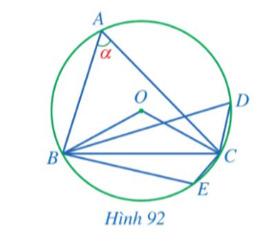
Trong Hình 92, cho các điểm A, B, C, D, E thuộc đường tròn (O).
a) Số đo góc BOC là
Xem lời giải »
Câu 4:
a) Độ dài cung tròn có số đo 30° của đường tròn bán kính R là:
Xem lời giải »
Câu 6:
Cho hai đường tròn (I; r) và (K; R) tiếp xúc ngoài với nhau tại P với R ≠ r, đường thẳng a lần lượt tiếp xúc với (I; r) và (K; R) tại A và B, a cắt KI tại O. Đường thẳng qua P vuông góc với IK cắt đường thẳng a tại M. Chứng minh:
a)
Xem lời giải »
Câu 8:
Mặt đĩa CD ở Hình 93 có dạng hình vành khuyên giới hạn bởi hai đường tròn có bán kính lần lượt là 1,5 cm và 6 cm. Hình vành khuyên đó có diện tích bằng bao nhiêu centimét vuông (làm tròn kết quả đến hàng đơn vị)?
Xem lời giải »