c) Mỗi tỉ số lượng giác của góc B bằng tỉ số lượng giác nào góc C?

Cho góc nhọn $\widehat{xBy}=\alpha .$ Xét tam giác ABC vuông tại A, tam giác A’BC’ vuông tại A’ với A, A’ thuộc tia Bx và C, C’ thuộc tia By (Hình 1). Do ∆ABC ᔕ ∆A’BC’ nên $\frac{AC}{BC}=\frac{A^{\text{'}}{C}^{\text{'}}}{B{C}^{\text{'}}}.$

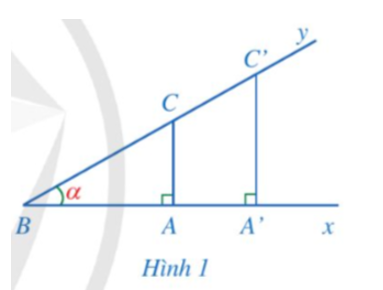
Như vậy, tỉ số giữa cạnh đối AC của góc nhọn α và cạnh huyền BC trong tam giác vuông ABC không phụ thuộc vào việc chọn tam giác vuông đó.

Tỉ số $\frac{AC}{BC}$ có mối liên hệ như thế nào với độ lớn góc α?

Cho tam giác ABC vuông tại A có $\widehat{B}=\alpha$ (Hình 2).

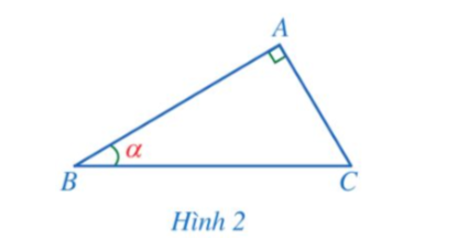
a) Cạnh góc vuông nào là cạnh đối của góc B?

b) Cạnh góc vuông nào là cạnh kề của góc B?

c) Cạnh nào là cạnh huyền?

a) sin61° – cos29°;

b) cos15° – sin75°;

c) tan28° – cot62°;

d) cot47° – tan43°.

Sử dụng bảng tỉ số lượng giác của các góc nhọn đặc biệt, tính giá trị của biểu thức:

sin60° – cos60°.tan60°.

Sử dụng tính chất cotα = tan(90° – α), ta có thể tính được côtang của một góc nhọn. Chẳng hạn ta tính cot56° như sau: