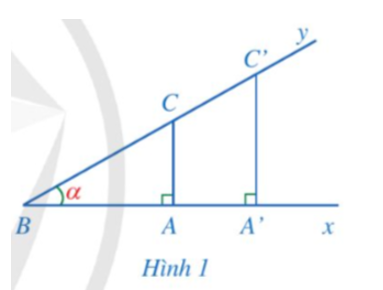
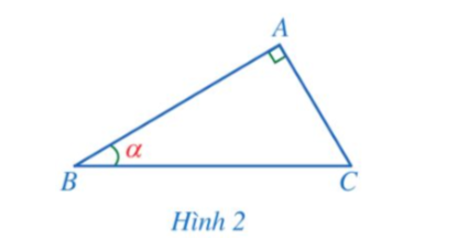
Sử dụng tính chất cotα = tan(90° – α), ta có thể tính được côtang của một góc nhọn.
Câu hỏi:
Sử dụng tính chất cotα = tan(90° – α), ta có thể tính được côtang của một góc nhọn. Chẳng hạn ta tính cot56° như sau:

Trả lời:
HS thực hiện hoạt động theo hướng dẫn của GV và SGK.