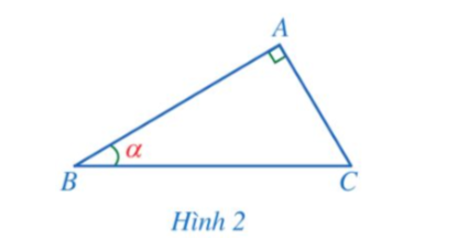
Cho tam giác ABC vuông tại A có AB = 2 cm, AC = 3 cm. Tính các tỉ số lượng giác của góc C.

Cho góc nhọn $\widehat{xBy}=\alpha .$ Xét tam giác ABC vuông tại A, tam giác A’BC’ vuông tại A’ với A, A’ thuộc tia Bx và C, C’ thuộc tia By (Hình 1). Do ∆ABC ᔕ ∆A’BC’ nên $\frac{AC}{BC}=\frac{A^{\text{'}}{C}^{\text{'}}}{B{C}^{\text{'}}}.$

Như vậy, tỉ số giữa cạnh đối AC của góc nhọn α và cạnh huyền BC trong tam giác vuông ABC không phụ thuộc vào việc chọn tam giác vuông đó.

Tỉ số $\frac{AC}{BC}$ có mối liên hệ như thế nào với độ lớn góc α?

Cho tam giác ABC vuông tại A có $\widehat{B}=\alpha$ (Hình 2).

a) Cạnh góc vuông nào là cạnh đối của góc B?

b) Cạnh góc vuông nào là cạnh kề của góc B?

c) Cạnh nào là cạnh huyền?

Cho tam giác MNP có MN = 5 cm, MP = 12 cm, NP = 13 cm. Chứng minh tam giác MNP vuông tại M. Từ đó, tính các tỉ số lượng giác của góc N.

Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63°? Vì sao?

a) sin27°;

b) cos27°;

c) tan27°;

d) cot27°.

Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):

a) 41°;

b) 28°35’;

c) 70°27’46’’.

Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giác trị biểu thức: A = sin25° + cos25° – sin65° – cos65°.