Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).
Câu hỏi:
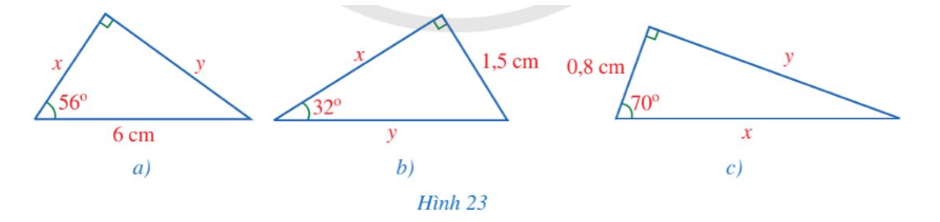
Tìm x, y trong mỗi hình 23a, 23b, 23c (làm tròn kết quả đến hàng phần mười của centimét).
Trả lời:
a) Từ hình ta có:
⦁ x = 6.cos56° ≈ 3,4 (cm).
⦁ y = 6.sin56° ≈ 5,0 (cm).
b) Từ hình ta có:
⦁ x = 1,5.cot32° ≈ 2,4 (cm).
⦁ 1,5 = y.sin32°, suy ra (cm).
c) Từ hình ta có:
⦁ 0,8 = x.cos70°, suy ra (cm).
⦁ y = 0,8.tan70° ≈ 2,2 (cm).