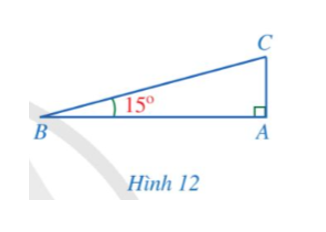
Tính độ cao AC trong Hình 12 khi BC = 20 m (làm tròn kết quả đến hàng phần mười của mét).
Câu hỏi:
Tính độ cao AC trong Hình 12 khi BC = 20 m (làm tròn kết quả đến hàng phần mười của mét).
Trả lời:
Xét ∆ABC vuông tại A, ta có: AC = BC.sinB = 20.sin15° ≈ 5,2 (m).
Xem thêm lời giải bài tập Toán 9 Cánh diều hay, chi tiết:
Câu 1:
Hình 12 mô tả đường lên dốc ở Hình 11, trong đó góc giữa BC và phương nằm giữa BA là
Cạnh góc vuông AC và cạnh huyền BC (Hình 12) có liên hệ với nhau như thế nào?
Xem lời giải »
Câu 2:
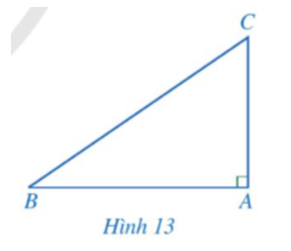
Cho tam giác ABC vuông tại A (Hình 13).
a) Biểu diễn sinB, cosC theo AC, BC.
Xem lời giải »
Câu 5:
Cho tam giác nhọn ABC có đường cao CK. Biểu diễn CK theo AC và sinA. Từ đó, chứng minh diện tích của tam giác ABC bằng
Xem lời giải »
Câu 6:
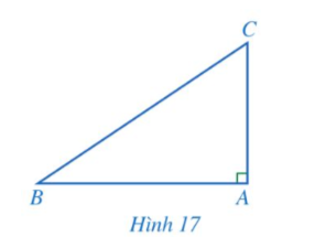
Cho tam giác ABC vuông tại A (Hình 17).
a) Biểu diễn tanB, cotC theo AB, AC.
Xem lời giải »