Giải Toán 9 trang 122 Tập 1 Cánh diều

---

Với Giải Toán 9 trang 122 Tập 1 trong Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 122.

Giải Toán 9 trang 122 Tập 1 Cánh diều

Hoạt động 6 trang 122 Toán 9 Tập 1:

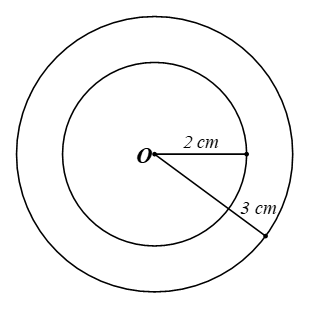
a) Hình 80 mô tả một phần bản vẽ của chi tiết máy. Hình đó giới hạn bởi mấy đường tròn cùng tâm?

b) Hãy vẽ một hình tương tự Hình 80 bằng cách vẽ các đường tròn (O; 2 cm) và (O; 3 cm). Tính hiệu diện tích của hai hình tròn đó.

Lời giải:

a) Hình chi tiết máy được giới hạn bởi hai đường tròn cùng tâm.

b)

Diện tích hình tròn tâm O bán kính 3 cm là: π.3² = 9π (cm²).

Diện tích hình tròn tâm O bán kính 2 cm là: π.2² = 4π (cm²).

Hiệu diện tích của hai hình tròn đó là: 9π – 4π = 5π (cm²).

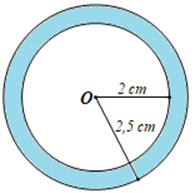
Luyện tập 5 trang 122 Toán 9 Tập 1: Tính diện tích của hình vành khuyên đó giới hạn bởi hai đường tròn cùng tâm và có bán kính lần lượt là 2,5 cm; 2 cm.

Lời giải:

Hình vành khuyên giới hạn bởi hai đường tròn cùng tâm O và có bán kính lần lượt là 2,5 cm; 2 cm được tô màu xanh như hình vẽ dưới đây:

Diện tích của hình vành khuyên tô màu xanh là: $S=\pi \left(2,5^2-2^2\right)=\frac{9\pi }{4}{\text{(cm}}^2\text{).}$

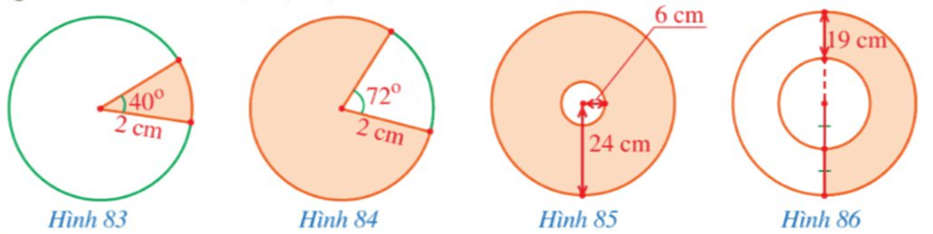
Bài 1 trang 122 Toán 9 Tập 1: Quan sát các hình 83, 84, 85, 86.

a) Tính diện tích phần được tô màu mỗi hình đó.

b) Tính độ dài cung tròn được tô màu xanh ở mỗi hình 83, 84.

Lời giải:

a) ⦁ Hình 83: Diện tích hình quạt tròn có bán kính 2 cm, số đo cung 40° là:

$S=\frac{\pi \cdot 2^2\cdot 40}{360}=\frac{4}{9}\pi {\text{(cm}}^2\text{).}$

Vậy diện tích phần được tô màu là: $\frac{4}{9}\pi {\text{(cm}}^2\text{).}$

⦁ Hình 84: Diện tích hình tròn có bán kính 2 cm là S₁ = π.2² = 4π (cm²).

Diện tích hình quạt tròn có bán kính 2 cm, số đo cung 72° là:

$S_2=\frac{\pi \cdot 2^2\cdot 72}{360}=\frac{4}{5}\pi {\text{(cm}}^2\text{).}$

Vậy diện tích phần được tô màu là: $S=S_1-S_2=4\pi -\frac{4}{5}\pi =\frac{16}{5}\pi {\text{(cm}}^2\text{).}$

⦁ Hình 85: Diện tích phần được tô màu chính là diện tích hình vành khuyên được giới hạn bởi hai đường tròn cùng tâm bán kính 24 cm và 6 cm, và bằng:

S = π.(24² – 6²) = 540π (cm²).

⦁ Hình 86: Đường tròn nhỏ bên trong có bán kính là 19 cm. Đường tròn to bên ngoài có bán kính là 2.19 = 38 cm.

Diện tích phần được tô màu chính là nửa diện tích hình vành khuyên được giới hạn bởi hai đường tròn cùng tâm có bán kính 38 cm và 19 cm, và bằng:

$S=\frac{1}{2}\pi \cdot \left({38}^2-{19}^2\right)=\frac{1083\pi }{2}{\text{(cm}}^2\text{).}$

b) Cách 1: Tính độ dài cung tròn theo công thức $l=\frac{\pi Rn}{180}.$

⦁ Hình 83: Số đo cung tròn được tô màu xanh là: 360° – 40° = 320°.

Độ dài cung tròn được tô màu xanh là: $l=\frac{\pi \cdot 2\cdot 320}{180}=\frac{32\pi }{9}\text{(cm)}.$

⦁ Hình 84: Độ dài cung tròn được tô màu xanh là: $l=\frac{\pi \cdot 2\cdot 72}{180}=\frac{4\pi }{5}\text{(cm).}$

Cách 2: Tính độ dài cung tròn theo diện tích của cung đó.

Ta có $S=\frac{lR}{2},$ do đó $l=\frac{2S}{R}.$

⦁ Hình 83: Diện tích của hình tròn bán kính 2 cm là π.2² = 4π (cm²).

Diện tích của phần không tô màu là: $S^{\text{'}}=4\pi -\frac{4}{9}\pi =\frac{32}{9}\pi {\text{(cm}}^2\text{).}$

Độ dài cung tròn được tô màu xanh là: $l=\frac{2\cdot \frac{32}{9}\pi }{2}=\frac{32\pi }{9}\text{(cm)}.$

⦁ Hình 84: Độ dài cung tròn được tô màu xanh là: $l=\frac{2\cdot \frac{4}{5}\pi }{2}=\frac{4}{5}\pi \text{(cm)}.$

Lời giải bài tập Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên hay khác:

• Giải Toán 9 trang 118

• Giải Toán 9 trang 119

• Giải Toán 9 trang 120

• Giải Toán 9 trang 123