Giải Toán 9 trang 90 Tập 1 Cánh diều

Với Giải Toán 9 trang 90 Tập 1 trong Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn Toán lớp 9 Cánh diều hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 90.

Giải Toán 9 trang 90 Tập 1 Cánh diều

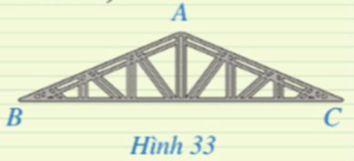
Luyện tập 2 trang 90 Toán 9 Tập 1: Mặt cắt đứng của khung thép có dạng tam giác cân ABC với $\hat{B}=23°,$ AB = 4 m (Hình 33). Tính độ dài đoạn thẳng BC (làm tròn kết quả đến hàng phần mười của mét).

Lời giải:

Kẻ AH ⊥ BC.

Vì ∆ABC cân tại A nên đường cao AH đồng thời là đường trung tuyến, do đó H là trung điểm của BC, nên BC = 2BH.

Xét ∆ABH vuông tại H, ta có: BH = AB.cosB = 4.cos23° ≈ 3,7 (m).

Do đó BC = 2BH ≈ 2.3,7 = 7,4 (m).

Vậy BC ≈ 7,4 m.

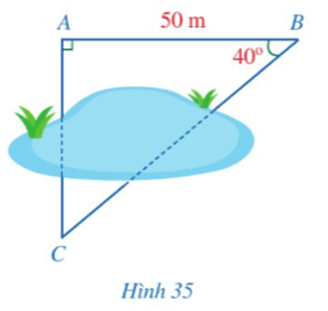
Bài 1 trang 90 Toán 9 Tập 1: Hình 35 mô tả ba vị trí A, B, C là ba đỉnh của một tam giác vuông và không đo được trực tiếp các khoảng cách từ C đến A và từ C đến B. Biết AB = 50 m, $\widehat{ABC}=40°.$ Tính các khoảng cách CA và BC (làm tròn kết quả đến hàng đơn vị của mét).

Lời giải:

Xét ∆ABC vuông tại A, ta có:

⦁ CA = AB.tan$\widehat{ABC}$ = 50.tan40^o $\approx$ 42(m).

⦁ AB = BC.cos$\widehat{ABC}$, suy ra BC = $\frac{AB}{\cos \widehat{ABC}}=\frac{50}{\cos 40°}\approx 65\text{(m).}$

Lời giải bài tập Toán 9 Bài 3: Ứng dụng của tỉ số lượng giác của góc nhọn hay khác:

• Giải Toán 9 trang 91