Giải Toán 9 trang 22 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 22 Tập 2 trong Bài tập cuối chương 6 Toán lớp 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 22.

Giải Toán 9 trang 22 Tập 2 Chân trời sáng tạo

Bài 3 trang 22 Toán 9 Tập 2: Cho hàm số y = 2x². Khi y = 2 thì

A. x = 1.

B. x = 2 hoặc x = −2.

C. x = 1 hoặc x = −1.

D. x = 2.

Lời giải:

Đáp án đúng là: C

Thay y = 2 vào y = 2x², ta được:

2x² = 2

x² = 1

x = ±1.

Vậy x = 1 hoặc x = −1.

Bài 4 trang 22 Toán 9 Tập 2: Đồ thị hàm số y = ax² (a ≠ 0) đi qua điểm (2; −2). Giá trị của a bằng

A. 2.

B. −2.

C. $\frac{1}{2}$.

D. $-\frac{1}{2}$.

Lời giải:

Đáp án đúng là: D

Thay x = 2; y = −2 vào y = ax², ta được −2 = a . 2² hay $a=-\frac{1}{2}.$

Bài 5 trang 22 Toán 9 Tập 2: Nghiệm của phương trình x² − 14x + 13 = 0 là

A. x₁ = −1; x₂ = 13.

B. x₁ = −1; x₂ = −13.

C. x₁ = 1; x₂ = −13.

D. x₁ = 1; x₂ = 13.

Lời giải:

Đáp án đúng là: D

Phương trình x² − 14x + 13 = 0 có a = 1, b = −14, c = 13.

Ta có Δ = (−7)² – 1 . 13 = 36 > 0.

Vậy phương trình có hai nghiệm phân biệt là: $x_1=\frac{7+\sqrt{36}}{1}=13;x_2=\frac{7-\sqrt{36}}{1}=1.$

Bài 6 trang 22 Toán 9 Tập 2: Phương trình nào dưới đây không là phương trình bậc hai một ẩn?

A. $x^2-\sqrt{7}x+7=0.$

B. 3x² + 5x – 2 = 0.

C. 2x² – 2 365 = 0.

D. –7x + 25 = 0.

Lời giải:

Đáp án đúng là: D

Phương trình –7x + 25 = 0 không phải phương trình bậc hai một ẩn vì –7x + 25 = 0 chính là phương trình 0x² – 7x + 25 = 0 với x² có hệ số a = 0.

Bài 7 trang 22 Toán 9 Tập 2: Gọi S và P lần lượt là tổng và tích của hai nghiệm của phương trình x² + 5x – 10 = 0. Khi đó giá trị của S và P là

A. S = 5; P = 10.

B. S = –5; P = 10.

C. S = –5; P = –10.

D. S = 5; P = –10.

Lời giải:

Đáp án đúng là: C

Ta có $S=x_1+x_2=-\frac{b}{a}=-5;P=x_1\cdot x_2=\frac{c}{a}=-10.$

Bài 8 trang 22 Toán 9 Tập 2: Cho phương trình x² + 7x – 15 = 0. Gọi x₁, x₂ là hai nghiệm của phương trình. Khi đó giá trị của biểu thức $x_1^2+x_2^2-x_1{x}_2$  là

A. 79.

B. 94.

C. –94.

D. –79.

Lời giải:

Đáp án đúng là: B

Phương trình x² + 7x – 15 = 0 có ∆ = 7² – 4 . 1 . (–15) = 109 > 0 nên nó có hai nghiệm phân biệt x₁, x₂.

Theo định lí Viète, ta có: $x_1+x_2=\frac{-b}{a}=-7;x_1\cdot x_2=\frac{c}{a}=-15.$

Ta có $x_1^2+x_2^2-x_1{x}_2=x_1^2+2x_1{x}_2+x_2^2-3x_1{x}_2$

$={\left(x_1+x_2\right)}^2-3x_1{x}_2$= (–7)² – 3 . (–15) = 94.

Vậy $x_1^2+x_2^2-x_1{x}_2=94.$

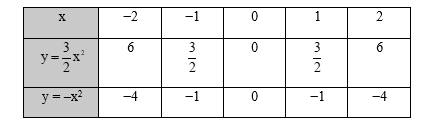
Bài 9 trang 22 Toán 9 Tập 2: Cho hai hàm số: $y=\frac{3}{2}{x}^2$ và y = –x². Vẽ đồ thị của hai hàm số đã cho trên cùng mặt phẳng tọa độ Oxy.

Lời giải:

Ta có bảng giá trị của hàm số:

Trên mặt phẳng tọa độ, lấy các điểm $A\left(-2;6\right),B\left(-1;\frac{3}{2}\right),O\left(0;0\right),C\left(1;\frac{3}{2}\right),D\left(2;6\right),$

A'(−2; −4), B'(−1; −1), C'(1; −1), D'(2; −4).

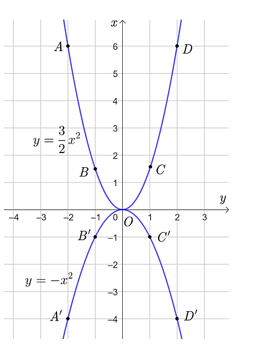
• Đồ thị hàm số $y=\frac{3}{2}{x}^2$  là một đường parabol đỉnh O, đi qua các điểm $B\left(-1;\frac{3}{2}\right),O\left(0;0\right),C\left(1;\frac{3}{2}\right),D\left(2;6\right).$

• Đồ thị hàm số y = –x² là một đường parabol đỉnh O, đi qua các điểm A'(−2; −4), B'(−1; −1), C'(1; −1), D'(2; −4).

Ta có đồ thị của hai hàm số hai hàm số $y=\frac{3}{2}{x}^2$  và y = –x² được vẽ trên cùng một mặt phẳng tọa độ Oxy như sau:

Bài 10 trang 22 Toán 9 Tập 2: Cho hàm số y = ax² (a ≠ 0)

a) Tìm a để đồ thị hàm số đi qua điểm M(2; 2).

b) Vẽ đồ thị (P) của hàm số với a vừa tìm được.

c) Tìm các điểm thuộc đồ thị (P) có tung độ y = 8.

Lời giải:

a) Thay x = 2; y = 2 vào hàm số y = ax² (a ≠ 0), ta được: 2 = a . 2² suy ra $a=\frac{1}{2}$ .

b) Từ câu a, ta có $a=\frac{1}{2}$ nên đồ thị hàm số cần tìm là $y=\frac{1}{2}{x}^2$ .

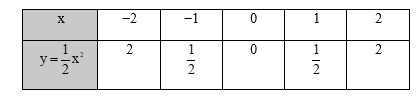
Ta có bảng giá trị:

Trên mặt phẳng tọa độ, lấy các điểm $A\left(-2;2\right),B\left(-1;\frac{1}{2}\right),O\left(0;0\right),B^{\text{'}}\left(1;\frac{1}{2}\right),A^{\text{'}}\left(2;2\right).$

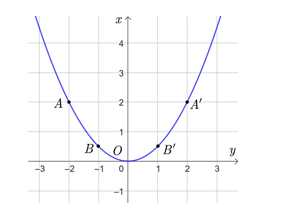
Đồ thị hàm số $y=\frac{1}{2}{x}^2$ là một đường parabol đỉnh O, đi qua các điểm trên và có dạng như dưới đây.

c) Thay y = 8 vào $y=\frac{1}{2}{x}^2$, ta được:

$8=\frac{1}{2}{x}^2$

x² = 16

x = ±4.

Vậy có hai điểm thuộc đồ thị là: (−4; 8), (4; 8).

Bài 11 trang 22 Toán 9 Tập 2: Giải các phương trình:

a) x² – 12x = 0;

b) 13x² + 25x – 38 = 0;

c) $3x^2-4\sqrt{3}x+4=0;$

d) x(x + 3) = 27 – (11 – 3x).

Lời giải:

a) x² – 12x = 0

x(x – 12) = 0

x = 0 hoặc x – 12 = 0

x = 0 hoặc x = 12.

Vậy phương trình có 2 nghiệm là x = 0 và x = 12.

b) 13x² + 25x – 38 = 0

Phương trình 13x² + 25x – 38 = 0 có a + b + c = 13 + 25 – 38 = 0.

Vậy phương trình có hai nghiệm là $x_1=1;x_2=\frac{c}{a}=-\frac{38}{13}.$

c) $3x^2-4\sqrt{3}x+4=0$

Ta có ${\Delta }^{\text{'}}={\left(-2\sqrt{3}\right)}^2-4\cdot 3=0$ .

Vậy phương trình có nghiệm kép $x_1=x_2=\frac{4\sqrt{3}}{2\cdot 3}=\frac{2\sqrt{3}}{3}.$

d) x(x + 3) = 27 – (11 – 3x)

x² + 3x = 27 – 11 + 3x

x² = 16

x = ±4.

Vậy phương trình có 2 nghiệm là x = ±4.

Lời giải bài tập Toán 9 Bài tập cuối chương 6 hay khác:

• Giải Toán 9 trang 21
• Giải Toán 9 trang 23