Giải Toán 9 trang 68 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 68 Tập 2 trong Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 68.

Giải Toán 9 trang 68 Tập 2 Chân trời sáng tạo

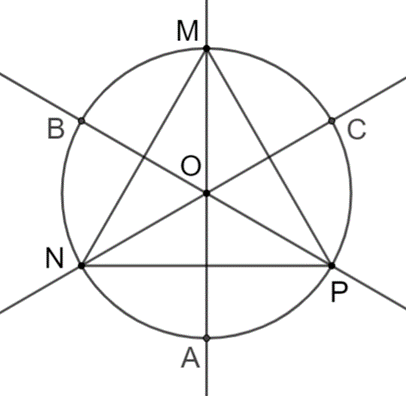
Thực hành 2 trang 68 Toán 9 Tập 2: Xác định tâm và bán kính đường tròn nội tiếp tam giác đều MNP có độ dài cạnh bằng 8 cm.

Lời giải:

Gọi O là giao điểm của đường cao MA, NP và PC của tam giác MNP.

Ta có tam giác MNP đều nên MA, NB, PC  là ba đường trung tuyến đồng thời là ba đường phân giác của tam giác.

Do đó, O là trọng tâm, đồng thời là tâm đường tròn nội tiếp tam giác MNP với bán kính r = OA = OB = OC.

Bán kính đường tròn ngoại tiếp tam giác là $r=\frac{1}{3}\cdot \frac{8\sqrt{3}}{2}=\frac{4\sqrt{3}}{3}\left(cm\right).$

Do đó, đường tròn nội tiếp tam giác đều MNP có tâm O và bán kính $r=\frac{4\sqrt{3}}{3}cm$ như hình vẽ.

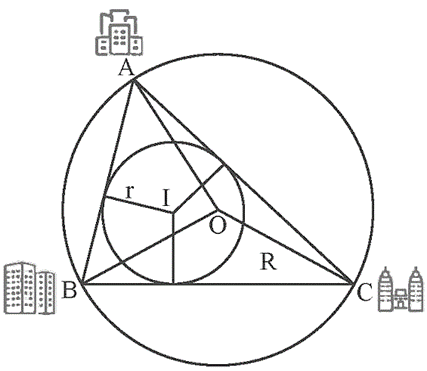
Vận dụng 2 trang 68 Toán 9 Tập 2: Theo gợi ý trong Hình 10, nêu cách xác định hai điểm I và O của tình huống trong Hoạt động khởi động (trang 65).

Lời giải:

− Vị trí điểm O để xây trường học cần cách đều 3 điểm A, B, C nên O là tâm đường tròn ngoại tiếp tam giác ABC.

− Vị trí điểm I để lập trạm cứu hộ cần cách đều 3 con đường AB, BC, CA nên I là tâm đường tròn nội tiếp tam giác ABC.

Bài 1 trang 68 Toán 9 Tập 2: Cho tam giác đều ABC có cạnh bằng 6 cm.

a) Nêu các vẽ đường tròn ngoại tiếp tam giác ABC.

b) Nêu các vẽ đường tròn nội tiếp tam giác ABC.

c) Tính bán kính R của đường tròn ngoại tiếp và bán kính r của đường tròn nội tiếp tam giác ABC.

Lời giải:

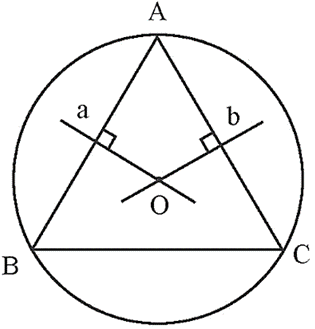
a) Cách vẽ đường tròn ngoại tiếp tam giác ABC:

− Vẽ đường trung trực a của đoạn thẳng AB.

− Vẽ đường trung trực b của đoạn thẳng AC.

− Gọi O là giao điểm của a và b.

− Vẽ đường tròn tâm O bán kính OA.

Khi đó, đường tròn (O; OA) là đường tròn ngoại tiếp tam giác ABC.

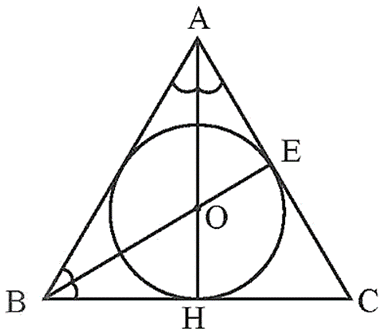
b) Cách vẽ đường tròn nội tiếp tam giác ABC:

− Vẽ đường phân giác AH của góc BAC.

− Vẽ đường phân giác BE của góc ABC.

− Gọi O là giao điểm của AH và BE.

− Vẽ đường tròn tâm O bán kính OH.

Khi đó, đường tròn (O; OH) là đường tròn nội tiếp tam giác ABC.

c) Vì tam giác ABC đều nên O cũng là trọng tâm của ∆ABC.

Theo định lí Pythagore, ta có: AB² = AH² + BH².

Suy ra $AH=\sqrt{AB{}^2-BH{}^2}=\sqrt{6{}^2-3{}^2}=3\sqrt{3}\left(cm\right).$

Bán kính đường tròn ngoại tiếp tam giác ABC là:

$R=OA=\frac{2}{3}AH=\frac{2}{3}\cdot 3\sqrt{3}=2\sqrt{3}\left(cm\right).$

Bán kính đường tròn nội tiếp tam giác ABC là:

$r=OH=\frac{1}{3}AH=\frac{1}{3}\cdot 3\sqrt{3}=\sqrt{3}\left(cm\right).$

Vậy $R=2\sqrt{3}cm;r=\sqrt{3}cm.$

Lời giải bài tập Toán 9 Bài 1: Đường tròn ngoại tiếp tam giác. Đường tròn nội tiếp tam giác hay khác:

• Giải Toán 9 trang 65

• Giải Toán 9 trang 67

• Giải Toán 9 trang 69