Giải Toán 9 trang 71 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 71 Tập 2 trong Bài 2: Tứ giác nội tiếp Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 71.

Giải Toán 9 trang 71 Tập 2 Chân trời sáng tạo

Thực hành 1 trang 71 Toán 9 Tập 2: Vẽ một tứ giác nội tiếp hình tròn và một tứ giác không nội tiếp đường tròn.

Lời giải:

Ta có thể vẽ tứ giác nội tiếp đường tròn và một tứ giác không nội tiếp đường tròn.

Chẳng hạn:

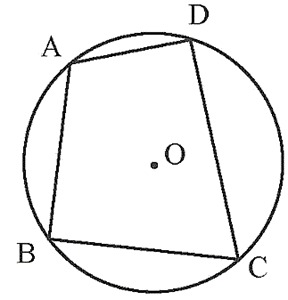
• Tứ giác ABCD nội tiếp đường tròn (O).

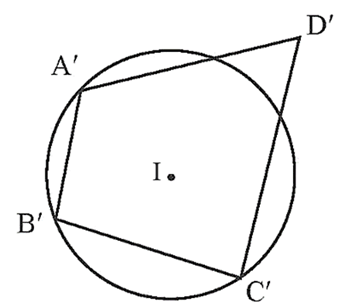
• Tứ giác A'B'C'D' không nội tiếp đường tròn (I).

Vận dụng 1 trang 71 Toán 9 Tập 2: Có nhận xét gì về tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn trong Hình 3.

Lời giải:

Trong Hình 3, tứ giác trong hình hoa văn trang trí mặt lưng của chiếc ghế với đường tròn  là tứ giác có các đỉnh đều nằm trên đường tròn nên là tứ giác nội tiếp.

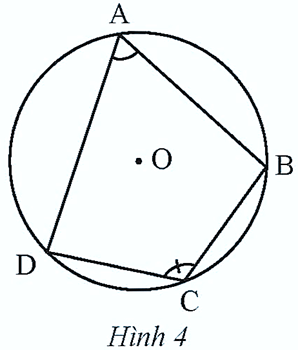
Khám phá 2 trang 71 Toán 9 Tập 2: Cho tứ giác ABCD nội tiếp đường tròn (O) (Hình 4).

a) Chỉ ra các cung chắn bởi mỗi góc nội tiếp $\widehat{DAB}$ và $\widehat{DCB}.$

b) Tính tổng số đo của các cung vừa tìm được.

c) Nêu kết luận về tổng số đo của hai góc $\widehat{DAB}$ và $\widehat{DCB}.$

d) Có nhận xét gì về tổng số đo của hai góc đối diện còn lại của tứ giác ABCD?

Lời giải:

a) Góc DAB là góc nội tiếp chắn cung BD nhỏ.

Góc DAB là góc nội tiếp chắn cung BD lớn.

b) Vì $\widehat{DAB}$ là góc nội tiếp chắn cung BD nhỏ nên $\widehat{DAB}$ bằng $\frac{1}{2}$ số đo cung BD nhỏ.

Vì $\widehat{DCB}$ là góc nội tiếp chắn cung BD lớn nên $\widehat{DCB}$ bằng $\frac{1}{2}$ số đo cung BD lớn.

Khi đó ta có: $\widehat{DAB}+\widehat{DCB}=\frac{1}{2}$ (số đo cung BD nhỏ + số đo cung BD lớn)

                                          = $\frac{1}{2}$.360^o = 180^o.

c) Tổng số đo của hai góc $\widehat{DAB}$ và $\widehat{DCB}$ bằng 180°.

d) Tổng số đo của hai góc đối diện còn lại của tứ giác ABCD là 180°

(vì 360° – 180° = 180°).

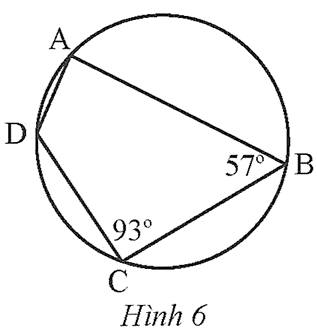
Thực hành 2 trang 71 Toán 9 Tập 2: Tìm số đo các góc chưa biết của tứ giác ABCD trong Hình 6.

Lời giải:

Tứ giác ABCD là tứ giác nội tiếp.

Suy ra $\widehat{A}+\widehat{C}=180°$; $\widehat{B}+\widehat{D}=180°$.

Do đó

$\widehat{A}=180°-\widehat{C}=180°-93°=87°;$ $\widehat{D}=180°-\widehat{B}=180°-57°=123°.$

Vậy $\widehat{A}=87°;\widehat{D}=123°.$

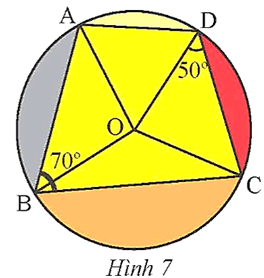
Vận dụng 2 trang 71 Toán 9 Tập 2: Trong hình vẽ minh họa của học sinh có một tứ giác ABCD nội tiếp đường tròn tâm O (Hình 7). Cho biết $\widehat{ABC}=70°,\widehat{ODC}=50°.$ Tìm góc $\widehat{AOD}.$

Lời giải:

Vì tứ giác ABCD nội tiếp đường tròn tâm O nên $\widehat{ABC}+\widehat{ADC}=180°$.

Suy ra $\widehat{ADC}=180°-\widehat{ABC}=180°-70°=110°.$

Mà $\widehat{ADO}+\widehat{OCD}=\widehat{ADC}$

nên $\widehat{ADO}=\widehat{ADC}-\widehat{OCD}=110°-50°=60°.$

Vì OA = OD = R nên tam giác OAD cân tại O.

Suy ra $\widehat{OAD}=\widehat{ADO}=60°$ (tính chất tam giác cân).

Do đó, tam giác OAD đều, suy ra $\widehat{AOD}=60°$.

Lời giải bài tập Toán 9 Bài 2: Tứ giác nội tiếp hay khác:

• Giải Toán 9 trang 70

• Giải Toán 9 trang 73

• Giải Toán 9 trang 74