Giải Toán 9 trang 90 Tập 2 Chân trời sáng tạo

---

Haylamdo biên soạn và sưu tầm lời giải bài tập Toán 9 trang 90 Tập 2 trong Bài 2: Hình nón Toán 9 Chân trời sáng tạo hay nhất, chi tiết sẽ giúp học sinh dễ dàng làm bài tập Toán 9 trang 90.

Giải Toán 9 trang 90 Tập 2 Chân trời sáng tạo

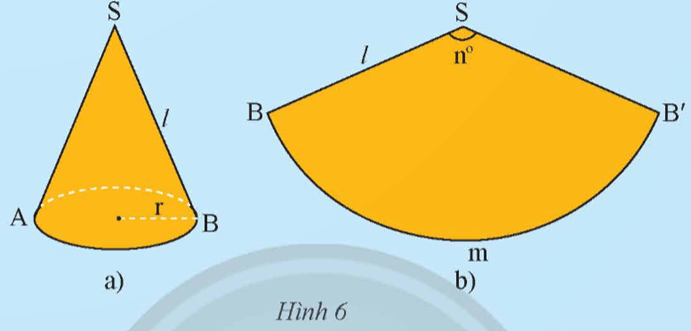
Khám phá 2 trang 90 Toán 9 Tập 2: Cho một hình nón có bán kính r, có độ dài đường sinh l (Hình 6a). Cắt mặt xung quanh của hình nón theo một đường sinh của nó rồi trải phẳng ra, ta được hình quạt tròn (Hình 6b). Tính theo r và l:

a) Độ dài cung BB';

b) Số đo cung BB';

c) Diện tích của hình quạt tròn.

Lời giải:

a) Độ dài m của cung BB' bằng chu vi đường tròn đáy, ta có m = 2πr.

b) Gọi n là số đo cung BB' của hình quạt tròn.

Áp dụng công thức liên hệ số đo cung n và độ dài cung m của hình quạt tròn, ta có:

n = $\frac{\text{m}\cdot 180}{\text{π}l}$ (với l là bán kính hình quạt tròn).

Số đo cung BB' là: n = $\frac{2\text{πr}\cdot 180}{\text{π}l}=\frac{360\text{r}}{l}.$

Vậy số đo cung BB' là n = $\frac{360\text{r}}{l}.$

c) Diện tích của hình quạt tròn là:

$\text{S}=\frac{\text{π\hspace{0.17em}}{l}^2\text{n}}{360}=\frac{\text{π\hspace{0.17em}}{l}^2\cdot \frac{360\text{r}}{l}}{360}=\frac{\text{π\hspace{0.17em}}l\cdot 360\text{r}}{360}=\text{πr\hspace{0.17em}}l.$

Vậy diện tích của hình quạt tròn là πrl.

Thực hành 3 trang 90 Toán 9 Tập 2: Tính diện tích xung quanh và diện tích toàn phần của hình nón có đường kính đáy d = 10 m và chiều cao h = 12 m (kết quả làm tròn đến hàng phần trăm).

Lời giải:

Bán kính đáy của hình nón là: r = $\frac{d}{2}=\frac{10}{2}$ = 5 (m).

Độ dài đường sinh của hình nón là:

$l=\sqrt{{\text{r}}^2+{\text{h}}^2}=\sqrt{5^2+{12}^2}=13\text{\hspace{0.17em}\hspace{0.17em}(m)}$

Diện tích xung quanh của hình nón là:

S_xq = πrl = π . 5 . 13 = 65π ≈ 204,20 (m²).

Diện tích đáy của hình nón là:

S_đáy = π . r² = π . 5² = 25π (m²).

Diện tích toàn phần của hình nón là:

S_tp = S_xq + S_đáy = 65π + 25π = 90π ≈ 282,74 (m²).

Vậy hình nón có diện tích xung quanh khoảng 204,20 m² và diện tích toàn phần khoảng 282,74 m².

Lời giải bài tập Toán 9 Bài 2: Hình nón hay khác:

• Giải Toán 9 trang 88

• Giải Toán 9 trang 89

• Giải Toán 9 trang 91

• Giải Toán 9 trang 92